Ejercicios

Ejercicios de Clase 01

Abra una terminal (consola) o notebook y utilícela como una calculadora para realizar las siguientes acciones:
- Suponiendo que, de las tres horas de clases, dedicamos dos períodos de media hora para que realicen ejercicios (de Python), dedicamos diez minutos a distraernos en un recreo, y el resto a la exposición ‘teórica’, calcular cuántos minutos efectivos de trabajo tendremos en las 13 clases.
- Calcule el porcentaje de horas del curso efectivamente dedicadas al trabajo.
- ¿Cómo se modifica el porcentaje anterior si incluimos el examen final?
- Para la cantidad de alumnos presentes en el aula: ¿cuántas horas-persona de trabajo hay involucradas en este curso?
Muestre en la consola de Ipython (o usando Jupyter Notebooks):
- el nombre de su directorio actual
- los archivos en su directorio actual
- Cree un subdirectorio llamado tmp
- si está usando Linux, muestre la fecha y hora
- Borre el subdirectorio tmp
Sabiendo que la velocidad de la luz es aproximadamente 300000 km/s y que un año luz se define como la distancia que recorre la luz en un año, usando la terminal de python o la notebook:

calcule cuántos kilómetros son nueve meses-luz,
considerando que la luz del sol tarda ocho minutos en llegar a la tierra, calcule a cuántos metros de la tierra está el sol.

Para cubos de lados de longitud L = 1, 3, y 5: calcule su superficie y su volumen.
Para esferas de radios r = 1, 3, 5 y 8, calcule su superficie y su volumen.
Fíjese si alguno de los valores: $x_1=0.49$, $x_2=0.50$, $x_3=0.51$ es un cero de la función $f(x)=x^{2} + x/2 - 1/2$, esto es $f(x_i)=0$ para $i=1,2$ o $3$ .
Para el número complejo $z= 1 + 0.5\ i$
- Calcular $z^2$ y $z^5$.
- Calcular los complejos conjugados de $z$ y $z^3$.
- Escribir un programa que escriba las frases:
  - “El conjugado de z=1+0.5i es 1-0.5j”
  - “El conjugado de z=(1+0.5i)^2 es …” (con el valor correspondiente)

Ejercicios de Clase 02

Escriba funciones que calculen:

El volumen de una esfera
El volumen de una caja de lados L1, L2, L3

Escriba una función que tome como argumentos tres valores: a, b, c y calcule los ceros (raíces) del polinomio $a x^{2}\, + b\, x + c$.
Considere un polígono regular de $N$ lados inscripto en un círculo de radio unidad:
- Escriba una función que tome como argumento el número de lados $N$ y calcule el ángulo interior del polígono regular correspondiente (por ejemplo el de un triángulo es 60 grados, de un cuadrado es 90 grados, y de un pentágono es 108 grados). Pruebe su función para valores de $N= 3, 5, 6, 8, 9, 10, 12$.
- ¿Puede calcular la longitud del lado de los polígonos regulares si se encuentran inscriptos en un círculo de radio unidad?

En todos los casos, pruebe las funciones escritas

.. image:: figuras/interior-angles-square.png

.. image:: figuras/interior-angles-pentagon.png

Para Entregar: Para la cadena de caracteres:

s = '''Aquí me pongo a cantar
Al compás de la vigüela,
Que el hombre que lo desvela
Una pena estraordinaria
Como la ave solitaria
Con el cantar se consuela.'''

Forme un nuevo string de 10 caracteres que contenga los 5 primeros y los 5 últimos del string anterior s. Imprima por pantalla el nuevo string.
Forme un nuevo string que contenga los 10 caracteres centrales de s (utilizando un método que pueda aplicarse a otros strings también). Imprima por pantalla el nuevo string.
Cuente la cantidad de veces que aparecen los substrings es, la, que, co, en los siguientes dos casos: distinguiendo entre mayúsculas y minúsculas, y no distinguiendo. Imprima el resultado.
Cambie todas las letras “m” por “n” y todas las letras “n” por “m” en s. Imprima el resultado por pantalla.

Utilizando funciones y métodos de strings en la cadena de caracteres:
```
s1='En un lugar de la Mancha de cuyo nombre no quiero acordarme'
```

Obtenga la cantidad de caracteres.
Imprima la frase anterior pero con cada palabra empezando en mayúsculas.
Cuente cuantas letras ‘a’ tiene la frase, ¿cuántas vocales tiene?

Centrado manual de frases
1. Utilizando la función len() centre una frase corta en una pantalla de 80 caracteres. Utilice la frase: “Un ejercicio con cadena de caracteres”
2. Agregue subrayado a la frase anterior
3. Escriba una función que centre y subraye una frase dada como argumento. Se espera obtener algo así:
```
Un ejercicio con cadena de caracteres
-------------------------------------
```
4. Repita el punto anterior utilizando métodos de strings

Ejercicios de Clase 03

Manejos de listas:
- Cree la lista N de longitud 50, donde cada elemento es un número entero de 1 a 50 inclusive (Ayuda: vea la expresión range).
- Invierta la lista.
- Extraiga de N una lista N1 que contenga sólo aquellos elementos que sean el cuadrado de algún número entero.
- Extraiga de N una lista N2 que contenga sólo aquellos elementos que sean iguales al $n^2-n$ para algún número entero $n$.
Ayuda: Puede resultar útil recordar el uso de comprensión de listas.
Cree una lista de la forma L = [1,3,5,...,17,19,19,17,...,3,1] (Ayuda: vea la expresión range).
Escriba una función que tome un número entero de tres cifras, y devuelva el mayor entero que se puede formar con esas cifras (Ayuda: considere convertir el número entero a otros tipos).
Construya una lista L2 con 2000 elementos, todos iguales a 0.0005. Imprima su suma utilizando la función sum y comparar con el resultado que arroja la función que existe en el módulo math para realizar suma de números de punto flotante.
Operación “rara” sobre una lista:
- Defina la lista L = [0,1]
- Realice la operación L.append(L)
- Ahora imprima L, e imprima el último elemento de L.
- Haga que una nueva lista L1 tenga el valor del último elemento de L y repita el inciso anterior.

De los primeros 100 números naturales imprimir aquellos que no son divisibles por ninguno de: 2, 3, 5 o 7.
Usando estructuras de control, calcule el valor de la suma:

\[s_{1} = \frac{1}{2} \left(\sum_{k=1}^{100}k^{-1} \right)\]

para los casos:
1. Incluyendo todos los valores de k
2. Incluyendo únicamente los valores pares de k.
Escriba una función que estime la suma

\[s_{2} = \sum_{k=1}^{\infty} \frac{(-1)^{k} (k+1)}{2 k^{3} + k^{2}}\]

La función toma como argumentos un error relativo $\epsilon$ deseado y devuelve el valor de la suma y el error relativo estimado. Pruebe su función para un valor $\epsilon=10^{-5}$

Escriba una función que tome como argumento un párrafo de texto y devuelva un string con el párrafo en un “cartel” de un cierto ancho:

cartelizar(parrafo, ancho)

Por ejemplo, para el texto:

s = "Ullam vel totam cum neque exercitationem ut. Quae omnis rerum sit reprehenderit accusamus. Molestiae molestiae sit totam sint. Neque pariatur temporibus ut minima accusantium. Ad perferendis natus nisi dolor. Et sint maiores exercitationem reiciendis ut ab et."

sout = cartelizar(s, 60)

debe devolver el string:

sout = '* ******************************************************** *\n* Ullam vel totam cum neque exercitationem ut. Quae omnis  *\n*  rerum sit reprehenderit accusamus. Molestiae molestiae  *\n*   sit totam sint. Neque pariatur temporibus ut minima    *\n*  accusantium. Ad perferendis natus nisi dolor. Et sint   *\n* ******************************************************** *'

que al imprimirlo se verá:

print(sout)

* ******************************************************** *
* Ullam vel totam cum neque exercitationem ut. Quae omnis  *
*  rerum sit reprehenderit accusamus. Molestiae molestiae  *
*   sit totam sint. Neque pariatur temporibus ut minima    *
*  accusantium. Ad perferendis natus nisi dolor. Et sint   *
* ******************************************************** *

En 1949, D. R. Kaprekar, un matemático de la India especializado en matemática recreacional, describió un algoritmo que consiste en:
1. Tomar un número de cuatro cifras
2. Reacomodar las cifras para obtener el mayor número posible
3. Obtener reacomodando las cifras también el menor posible
4. Restarlos
5. GOTO 1
Este algoritmo tiene un “punto fijo” igual a 6174 y es al que el algoritmo llega si se inicia con un número que no tiene las cifras repetidas. Si alguna cifra es repetida el punto fijo puede ser el trivial, igual a cero. Escribir una función rutina_kaprekar(numero) que tome un número de cuatro cifras y devuelva el punto fijo y el número de números necesarios hasta alcanzarlo.

Por ejemplo: Para el número 1392, la secuencia es:

1392 -> 8082 -> 8532 -> 6174 -> 6174 -> …

por lo que tendremos al aplicar la función:
```
rutina_kaprekar(1392)
```
```
6174, 4
```

Consejo

Tenga en cuenta que si un número tiene menos de cuatro cifras debe agregarle ceros. Por ejemplo el número 978 debe entenderse como 0978 por lo que el mayor número que puede escribirse con estas cifras es 9870.

Escribir, utilizando conjuntos (set), funciones que tomen como argumento un string y:

Retorne verdadero si el argumento tiene algún número, Falso en otro caso,
Retorne verdadero si el argumento está formado por todos números, Falso en otro caso.

Ejercicios de Clase 04

Defina una función que dada una altura inicial h_0, una velocidad inicial v_0 y un paso de tiempo delta_t, devuelva:
- una lista conteniendo los tiempos de cálculo,
- otra lista con las posiciones h(t) (alturas) de la partícula en función del tiempo.
- una tercer lista con las velocidades v(t) de la partícula en cada instante.
Use las funciones definidas en la clase
Escriba una función imprime_trayectoria que, obviamente, imprime la trayectoria h(t) en forma clara y bella. Para esto puede resultarle útil la función `zip <https://docs.python.org/3.3/library/functions.html#zip>`__.
Escriba funciones para analizar la divisibilidad de enteros:
- La función es_divisible que retorna True si el argumento x es divisible por alguno de los elemntos del segundo argumento: divisores. El argumento divisores es opcional y si está presente es una variable del tipo lista que contiene los valores para los cuáles debemos examinar la divisibilidad.
  
  El valor por defecto de divisores es [2,3,5,7]. Las siguientes expresiones deben retornar el mismo valor:
```
es_divisible(x)
es_divisible(x, [2,3,5,7])
```
- La función es_divisible_por cuyo primer argumento (mandatorio) es x, y luego puede aceptar un número indeterminado de argumentos:
```
es_divisible_por(x)  # retorna verdadero siempre
es_divisible_por(x, 2) # verdadero si x es par
es_divisible_por(x, 2, 3, 5, 7) # igual resultado que es_divisible(x)
es_divisible_por(x, 2, 3, 5, 7, 9, 11, 13)  # o cualquier secuencia de argumentos debe funcionar
```
PARA ENTREGAR. Describimos una grilla de sudoku como un string de nueve líneas, cada una con 9 números, con números entre 1 y 9. Escribir un conjunto de funciones que permitan chequear si una grilla de sudoku es correcta. Para que una grilla sea correcta deben cumplirse las siguientes condiciones
- Los números están entre 1 y 9
- En cada fila no deben repetirse
- En cada columna no deben repetirse
- En todas las regiones de 3x3 que no se solapan, empezando de cualquier esquina, no deben repetirse
1. Escribir una función que convierta un string con formato a una lista bidimensional. El string estará dado con nueve números por línea, de la siguiente manera (los espacios en blanco en cada línea pueden variar):
```
sudoku = """145327698
        839654127
        672918543
        496185372
        218473956
        753296481
        367542819
        984761235
        521839764"""
```
1. Escribir una función check_repetidos() que tome por argumento una lista (unidimensional) y devuelva verdadero si la lista tiene elementos repetidos y falso en caso contrario.
2. Escribir la función check_sudoku() que toma como argumento una grilla (como una lista bidimensional de 9x9) y devuelva verdadero si los números corresponden a la resolución correcta del Sudoku y falso en caso contrario. Note que debe verificar que los números no se repiten en filas, ni en columnas ni en recuadros de 3x3. Para obtener la posición de los recuadros puede investigar que hacen las líneas de código:
```
j, k = (i // 3) * 3, (i % 3) * 3
r = [grid[a][b] for a in range(j, j+3) for b in range(k, k+3)]
```
suponiendo que grid es el nombre de nuestra lista bidimensional, cuando i toma valores entre 0 y 8.

Nota

Enviar por correo electrónico con el archivo adjunto nombrado en la forma 04_Apellido.py donde “Apellido” es su apellido.

Ejercicios de Clase 05

Escriba una función crear_sen(A, w) que acepte dos números reales $A, w$ como argumentos y devuelva la función f(x).

Al evaluar la función f en un dado valor $x$ debe dar el resultado: $f(x) = A \sin(w x)$ tal que se pueda utilizar de la siguiente manera:

from math import pi
f = crear_sen(3, 2)
f(pi/2)
# Debería imprimir el resultado de 3*sin(2 * pi/2) aprox. cero

Escriba una serie de funciones que permitan trabajar con polinomios. Vamos a representar a un polinomio como una lista de números reales, donde cada elemento corresponde a un coeficiente que acompaña una potencia. En cada caso elija los argumentos que considere necesario.
- Una función que devuelva el orden del polinomio (un número entero)
- Una función que sume dos polinomios y devuelva un polinomio (objeto del mismo tipo)
- Una función que multiplique dos polinomios y devuelva el resultado en otro polinomio
- Una función devuelva la derivada del polinomio (otro polinomio).
- Una función que acepte el polinomio y devuelva la función correspondiente.
Escriba una función direccion_media(ang1, ang2, ...) cuyos argumentos son direcciones en el plano, expresadas por los ángulos en grados a partir de un cierto eje, y calcule la dirección promedio, expresada en ángulos. Pruebe su función con las listas:
```
a1 = direccion_media(0, 180, 370, 10)
a2 = direccion_media(30, 0, 80, 180)
a3 = direccion_media(80, 180, 540, 280)
```
Las funciones de Bessel de orden $n$ cumplen las relaciones de recurrencia

\[J_{n -1}(x)- \frac{2n }{x}\, J_{n }(x) + J_{n +1}(x) = 0\]

\[J^{2}_{0}(x) + \sum_{n=1}^{\infty} 2 J^{2}_{n}(x) = 1\]

Para calcular la función de Bessel de orden $N$, se empieza con un valor de $M \gg N$, y utilizando los valores iniciales $J_{M}=1$, $J_{M+1}=0$ se utiliza la primera relación para calcular todos los valores de $n < M$. Luego, utilizando la segunda relación se normalizan todos los valores.

Nota

Estas relaciones son válidas si $M \gg x$ (use algún valor estimado, como por ejemplo $M=N+20$).

Utilice estas relaciones para calcular $J_{N}(x)$ para $N=3,4,7$ y $x=2.5, 5.7, 10$. Para referencia se dan los valores esperados

\[\begin{split}\begin{align} J_3( 2.5) = 0.21660\\ J_4( 2.5) = 0.07378\\ J_7( 2.5) = 0.00078\\ J_3( 5.7) = 0.20228\\ J_4( 5.7) = 0.38659\\ J_7( 5.7) = 0.10270\\ J_3(10.0) = 0.05838\\ J_4(10.0) = -0.21960\\ J_7(10.0) = 0.21671\\ \end{align}\end{split}\]
Dada una lista de números, vamos a calcular valores relacionados a su estadística.
- Realizar una función calc_media(x, que="aritmetica") que calcule los valores de la media aritmética, la media geométrica o la media armónica dependiendo del valor del argumento que. Las medias están dadas por:
  
  \[A(x_1, \ldots, x_n) = \bar{x} = \frac{x_1 + \cdots + x_n}{n}\]
  
  \[G(x_1, \ldots, x_n) = \sqrt[n]{x_1 \cdots x_n}\]
  
  \[H(x_1, \ldots, x_n) = \frac{n}{\frac{1}{x_1} + \cdots + \frac{1}{x_n}}\]
- Realizar una función que calcule la mediana de una lista de números (el argumento en este caso es del tipo list). La mediana se define como el valor para el cual la mitad de los valores de la lista es menor que ella. Si el número de elementos es par, se toma el promedio entre los dos adyacentes.
Realizar los cálculos para las listas de números:
```
L1 = [6.41, 1.28, 11.54, 5.13, 8.97, 3.84, 10.26, 14.1, 12.82, 16.67, 2.56, 17.95, 7.69, 15.39]
L2 = [4.79, 1.59, 2.13, 4.26, 3.72, 1.06, 6.92, 3.19, 5.32, 2.66, 5.85, 6.39, 0.53]
```
- La moda se define como el valor que ocurre más frecuentemente en una colección. Note que la moda puede no ser única. En ese caso debe obtener todos los valores. Escriba una función que retorne la moda de una lista de números. Utilícela para calcular la moda de la siguiente lista de números enteros:
```
L = [8, 9, 10, 11, 10, 6, 10, 17, 8, 8, 5, 10, 14, 7, 9, 12, 8, 17, 10, 12, 9, 11, 9, 12, 11, 11, 6, 9, 12, 5, 12, 9, 10, 16, 8, 4, 5, 8, 11, 12]
```
El módulo time calcula el tiempo en segundos desde el comienzo de la era de la computación (?), que para los fines prácticos, da inicio el 1 de enero de 1970 ;-D. Veamos unos ejemplos de su uso:

import time

ahora = time.time()
print (ahora)
# duerme 5 segundos
time.sleep(5) # zzzz.....

ahora = time.time()
print (ahora)

1740427615.6264267
1740427620.6271527

Utilizando las funciones anteriores, escriba el decorador @time_me que calcula e imprime el tiempo que tarda en ejecutarse una función. No empiece desde cero!! Use como plantilla para empezar el decorador @debug_me y modifíquelo adecuadamente.

# descomente el decorador una vez que lo tenga programado
# @time_me
def mi_calculo_recontralargo(n):
    l= [x for x in range(n)]
    return sum(l)

mi_calculo_recontralargo(20000000)

199999990000000

Construya una función partition(lst,predicate) que dada una lista lst y una función predicate, separe la lista lst en dos: una lista que contiene los valores para los cuales la función predicate devuelve True, y otra lista que contiene los valores para los que predicate devuelve False:
```
def is_even(x):
    return x % 2 == 0

numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
evens, odds = divide_list(numbers, is_even)

print(evens) # Output: [2, 4, 6, 8, 10]
print(odds)  # Output: [1, 3, 5, 7, 9]
```
Dado la cadena de caracteres
```
s1='En un lugar de la Mancha de cuyo nombre no quiero acordarme'
```
Utilice reduce, map y/o filter (y las funciones auxiliares necesarias) para:
- Obtener la cantidad de caracteres.
- Imprimir la frase anterior pero con cada palabra empezando en mayúsculas.
- Contar cuantas letras ‘a’ tiene la frase.
- Contar cuántas vocales tiene.

Ejercicios de Clase 06

Implemente los métodos suma, producto y norma
- suma debe retornar un objeto del tipo Vector y contener en cada componente la suma de las componentes de los dos vectores que toma como argumento.
- producto toma como argumentos dos vectores y retorna un número real con el valor del producto interno
- norma toma como argumentos el propio objeto y retorna el número real correspondiente:
  
  \[\sqrt{x^2 + y^2 + z^2}\]
Su uso será el siguiente:
```
v1 = Vector(1,2,3)
v2 = Vector(3,2,1)
vs1 = v1.suma(v2)
vs2 = v2.suma(v1)
print(type(vs2))
# print(vs1 == vs2)
pr = v1.producto(v2)
a = v1.norma()
```
Utilizando la definición de la clase Punto

class Punto:
  "Clase para describir un punto en el espacio"

  num_puntos = 0

  def __init__(self, x=0, y=0, z=0):
    "Inicializa un punto en el espacio"
    self.x = x
    self.y = y
    self.z = z
    Punto.num_puntos += 1
    return None

  def __del__(self):
    "Borra el punto y actualiza el contador"
    Punto.num_puntos -= 1

  def __str__(self):
    return f"Punto en el espacio con coordenadas: x = {self.x}, y = {self.y}, z = {self.z}"

  def __repr__(self):
    return f"Punto(x = {self.x}, y = {self.y}, z = {self.z})"

  def __call__(self):
    return self.__str__()

  @classmethod
  def total(cls):
    "Imprime el número total de puntos"
    print(f"En total hay {cls.num_puntos} puntos definidos")

Complete la implementación de la clase Vector con los métodos pedidos

class Vector(Punto):
  "Representa un vector en el espacio"

  def __add__(self, v2):
    "Calcula un vector que contiene la suma de dos vectores"
    print("Aún no implementada la suma de dos vectores")
    # código calculando v = suma de self + v2
    # ...

  def __mul__(self, v2):
    "Calcula el producto interno entre dos vectores"
    print("Aún no implementado el producto interno de dos vectores")
    # código calculando el producto interno pr = v1 . v2

  def __abs__(self):
    "Devuelve la distancia del punto al origen"
    print("Aún no implementado la norma del vector")
    # código calculando la magnitud del vector

  def angulo_entre_vectores(self, v2):
    "Calcula el ángulo entre dos vectores"
    print("Aún no implementado el ángulo entre dos vectores")
    angulo = 0
    # código calculando angulo = arccos(v1 * v2 / (|v1||v2|))
    return angulo

  def coordenadas_cilindricas(self):
    "Devuelve las coordenadas cilindricas del vector como una tupla (r, theta, z)"
    print("No implementada")

  def coordenadas_esfericas(self):
    "Devuelve las coordenadas esféricas del vector como una tupla (r, theta, phi)"
    print("No implementada")

PARA ENTREGAR: Cree una clase Polinomio para representar polinomios. La clase debe guardar los datos representando todos los coeficientes. El grado del polinomio será menor o igual a 9 (un dígito).

Nota

Utilice el archivo 06_polinomio.py en el directorio data, que renombrará de la forma usual 06_Apellido.py. Se le pide que programe:

Un método de inicialización __init__ que acepte una lista de coeficientes. Por ejemplo para el polinomio $4 x^3 + 3 x^2 + 2 x + 1$ usaríamos:

>>> p = Polinomio([1,2,3,4])

Un método grado que devuelva el orden del polinomio

>>> p = Polinomio([1,2,3,4])
>>> p.grado()
3

Un método get_coeficientes, que devuelva una lista con los coeficientes:

>>> p.get_coeficientes()
[1, 2, 3, 4]

Un método set_coeficientes, que fije los coeficientes de la lista:

>>> p1 = Polinomio()
>>> p1.get_coeficientes()
[]
>>> p1.set_coeficientes([1, 2, 3, 4])
>>> p1.get_coeficientes()
[1, 2, 3, 4]

El método __add__(self,pol2) que le sume otro polinomio y devuelva un polinomio (objeto del mismo tipo) Eso permitirá usar la operación de suma en la forma:

>>> p1 = Polinomio([1,2,3,4])
>>> p2 = Polinomio([1,2,3,4])
>>> p1 + p2

El método kmul(self, k) que multiplica al polinomio por una constante k y devuelve un nuevo polinomio
El método __mul__(self, pol2) que multiplica dos polinomios y devuelve un nuevo polinomio
Un método, derivada(n), que devuelva la derivada de orden n del polinomio (otro polinomio):

>>> p1 = p.derivada()
>>> p1.get_coeficientes()
[2, 6, 12]
>>> p2 = p.derivada(n=2)
>>> p2.get_coeficientes()
[6, 24]

Un método que devuelva la integral (antiderivada) del polinomio de orden n, con constante de integración cte (otro polinomio).

>>> p1 = p.integrada()
>>> p1.get_coeficientes()
[0, 1, 1, 1, 1]
>>>
>>> p2 = p.integrada(cte=2)
>>> p2.get_coeficientes()
[2, 1, 1, 1, 1]
>>>
>>> p3 = p.integrada(n=3, cte=1.5)
>>> p3.get_coeficientes()
[1.5, 1.5, 0.75, 0.16666666666666666, 0.08333333333333333, 0.05]

Un método from_string(expr) (pida ayuda si se le complica) que crea un polinomio desde un string en la forma:

>>> p = Polinomio()
>>> p.from_string('x^5 + 3x^3 - 2 x+x^2 + 3 - x')
>>> p.get_coeficientes()
[3, -3, 1, 3, 0, 1]
>>>
>>> p1 = Polinomio()
>>> p1.from_string('y^5 + 3y^3 - 2 y + y^2+3', var='y')
>>> p1.get_coeficientes()
[3, -2, 1, 3, 0, 1]

Escriba un método llamado __str__, que devuelva un string (que define cómo se va a imprimir el polinomio). Un ejemplo de salida será:

>>> p = Polinomio([1,2.1,3,4])
>>> print(p)
4 x^3 + 3 x^2 + 2.1 x + 1

Escriba un método llamado __call__, de manera tal que al llamar al objeto, evalúe el polinomio en un dado valor de x

>>> p = Polinomio([1,2,3,4])
>>> p(x=2)
49
>>>
>>> p(0.5)
3.25

Ejercicios de Clase 07

Realice un programa que:

Lea el archivo names.txt
Guarde en un nuevo archivo (llamado “pares.txt”) palabra por medio del archivo original (la primera, tercera, …) una por línea, pero en el orden inverso al leído
Agregue al final de dicho archivo, las palabras pares pero separadas por un punto y coma (;)
En un archivo llamado “longitudes.txt” guarde las palabras ordenadas por su longitud, y para cada longitud ordenadas alfabéticamente.
En un archivo llamado “letras.txt” guarde sólo aquellas palabras que contienen las letras w,x,y,z, con el formato:
- w: Walter, ….
- x: Xilofón, …
- y: ….
- z: ….
Cree un diccionario, donde cada key es la primera letra y cada valor es una lista, cuyo elemento es una tuple (palabra, longitud). Por ejemplo:

d['a'] = [('Aaa',3),('Anna', 4), ...]

Realice un programa para:
- Leer los datos del archivo aluminio.dat y poner los datos del elemento en un diccionario de la forma:
```
d = {'S': 'Al', 'Z':13, 'A':27, 'M': '26.98153863(12)', 'P': 1.0000, 'MS':'26.9815386(8)'}
```
- Modifique el programa anterior para que las masas sean números (float) y descarte el valor de la incerteza (el número entre paréntesis)
- Agregue el código necesario para obtener una impresión de la forma:
```
Elemento: Al
Número Atómico: 13
Número de Masa: 27
Masa: 26.98154
```

Note que la masa sólo debe contener 5 números decimales

Ejercicios de Clase 08

Cree una nueva clase Materia que describa una materia que se dicta en el IB. La clase debe contener información sobre el nombre de la materia, los alumnos que la cursan, y los docentes que la dictan. Utilice las clases Persona y Estudiante y, si es necesario, cree nuevas clases. Además debe proveer los siguientes métodos:
- agrega_estudiante que agrega un estudiante al curso
- agrega_docente que agrega un docente al curso
- imprime_estudiantes que lista los estudiantes del curso
El archivo atomos_t.json contiene datos atómicos y físicos de los primeros átomos de la tabla periódica. Se puede usar el módulo json para leer este archivo de la siguiente manera
```
import json
with open('atomos_t.json', 'r') as file:  # Verifique que el path al archivo sea el correcto en su caso
    atomos = json.load(file)
```
De esta manera se crea un diccionario atomos con la información del archivo.
- Cree una dataclass para manejar los datos atómicos, que incluya el nombre del elemento, el símbolo, el número atómico y la masa atómica.
- Extienda la clase anterior para poder manejar el estado del material a temperatura ambiente (‘State at Room Temp’). Para ello cree un enum adecuado para representarlo y construya una nueva dataclass adecuada.
- Modifique __repr__ y __str__ para que se imprima la información de cada átomo en forma clara y bella.
- ¿Qué estrategia/s usaría para incorporar las temperaturas de fusión (‘Melting Point’) y de ebullición (‘Boiling Point’) de los átomos de la lista?

Ejercicios de Clase 09

PARA ENTREGAR: En el ejercicio 08 se creó la clase Materia que describa una materia que se dicta en el IB. En dicha clase también se usaron las clases Persona y Estudiante. La clase Materia provee los siguientes métodos:
- agrega_estudiante que agrega un estudiante al curso
- agrega_docente que agrega un docente al curso
- imprime_estudiantes que lista los estudiantes del curso
Vamos a asumir que los estudiantes son alumnos de grado, de modo tal que las carreras posibles son Ingeniería (Nuclear, Mecánica o Telecomunicaciones) o Física, o son estudiantes vocacionales. En este ejercicio le pedimos que:
- Corrija la clase Estudiante de forma tal que sólo se puedan registrar estudiantes de grado de las carreras mencionadas, o estudiantes vocacionales.
- Extienda la clase Materia de modo tal que se pueda registrar la nota de cada estudiante al finalizar el curso.
- Cree la clase Admin que permita imprimir los listados de estudiantes de una materia y pueda expedir certificados de aprobación que contengan el nombre del alumno, el nombre de la materia y la nota obtenida en números y en letras. (El certificado es un archivo de texto con la información mencionada).
- Finalmente, modifique las clases anteriores de forma tal que se puedan crear y manejar materias a través de distintos años.
Organice el código en distintos módulos dentro de un proyecto, con un main.py donde se utilicen, a modo de ejemplo, las distintas características del código solicitadas.

Para entregar el ejercicio, cree un repositorio privado en GitHub conteniendo el proyecto con el nombre ‘modelo-materias-ib’ y agregue como colaborador a cursopythonib.
Un ejercicio interesante de aplicación de expresiones regulares(*) consiste en encontrar los coeficientes y las potencias de un polinomio que viene descripto como un string:
```
polinomio = "5x^4 + 3x^2 - 2x + 7"
```

Ejercicios de Clase 10

Genere arrays en 2d, cada uno de tamaño 10x10 con:
1. Un array con valores 1 en la “diagonal principal” y 0 en el resto (Matriz identidad).
2. Un array con valores 0 en la “diagonal principal” y 1 en el resto.
3. Un array con valores 1 en los bordes y 0 en el interior.
4. Un array con números enteros consecutivos (empezando en 1) en los bordes y 0 en el interior.
Diga qué resultado produce el siguiente código, y explíquelo

# Ejemplo propuesto por Jake VanderPlas
print(sum(range(5),-1))
from numpy import *
print(sum(range(5),-1))

Escriba una función suma_potencias(p, n) (utilizando arrays y Numpy) que calcule la operación

\[s_{2} = \sum_{k=0}^{n}k^{p}\]

.
Usando las funciones de numpy sign y maximum definir las siguientes funciones, que acepten como argumento un array y devuelvan un array con el mismo shape:

función de Heaviside, que vale 1 para valores positivos de su argumento y 0 para valores negativos.
La función escalón, que vale 0 para valores del argumento fuera del intervalo $(-1,1)$ y 1 para argumentos en el intervalo.
La función rampa, que vale 0 para valores negativos de $x$ y $x$ para valores positivos.

Ejercicios de Clase 11

Realizar un programa para visualizar la función

\[f(x,n,w) = x^n |\sin(w x)|\]

El programa debe realizar el gráfico para $w=10$, con cuatro curvas para $n=1,2,3,4$, similar al que se muestra en la siguiente figura
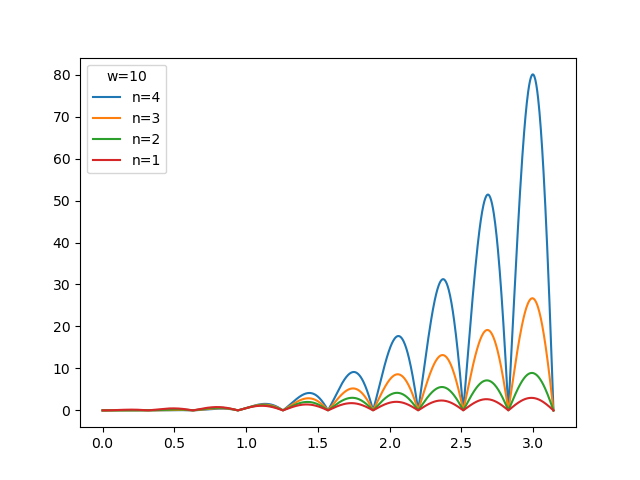
Para la función definida a trozos:

\[\begin{split}f(x) = \begin{cases} f_{1}(x) = x^{2}/8 & - \pi < x \le \pi/2 \\ f_{2}(x) = -0.3 x & \pi/2 < x < \pi \\ f_{3}(x) = -(x - 2 \pi)^{2}/6 & \pi \le x \le 5 \pi/2 \\ f_{4}(x) = (x - 2 \pi)/5 & 5 \pi/2 < x \le 3 \pi \end{cases}\end{split}\]

realizar la siguiente figura de la manera más fiel posible.

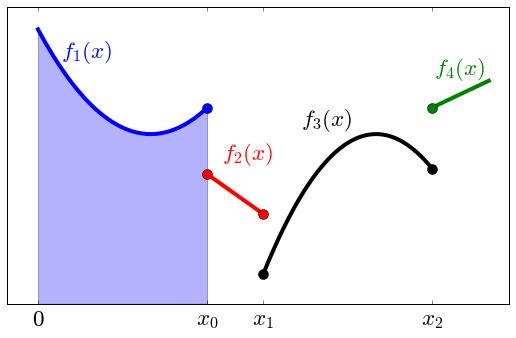
Pistas: Buscar información sobre plt.text(), plt.fill_between() y sobre plt.xticks y plt.yticks.
Rehacer la siguiente figura:
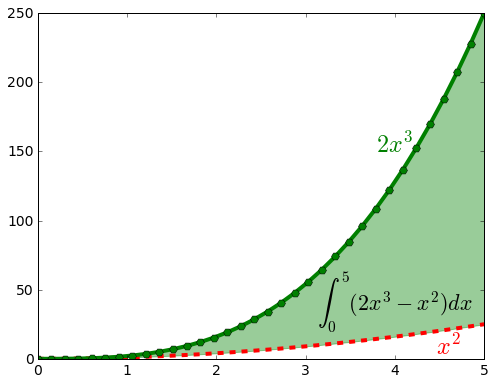
Notando que la curva en color negro corresponde a la suma de las dos curvas en rojo, rehacer la siguiente figura:
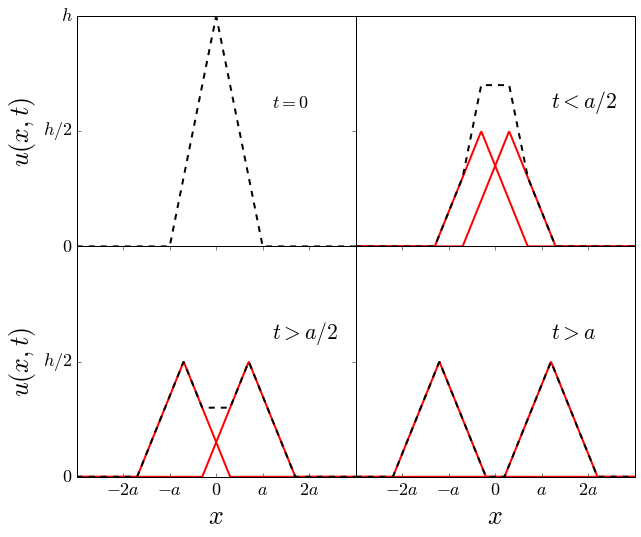
Crear una hoja de estilo que permita hacer gráficos adecuados para posters y presentaciones. Debe modificar los tamaños para hacerlos legibles a mayores distancias (sugerencia 16pt). El tamaño de la letra de los nombres de ejes y en las leyendas debe ser mayor también. Las líneas deben ser más gruesas (sugerencia: ~4), los símbolos de mayor tamaño (sugerencia ~10).

Ejercicios de Clase 12

Escribir una función mas_cercano(a, x) que tome dos argumentos: un array a y un escalar x, y devuelva el número de a más cercano a x. Utilice los métodos discutidos.

Pruebe la función con un array a de números, creado usando:
```
a = np.random.uniform(size=100)
```
y un valor x=0.5.
Cree una función que calcule la posición y velocidad de una partícula en caída libre para condiciones iniciales dadas ($h_{0}$, $v_{0}$), y un valor de gravedad dados. Se utilizará la convención de que alturas y velocidades positivas corresponden a vectores apuntando hacia arriba (una velocidad positiva significa que la partícula se aleja de la tierra).
- La función debe realizar el cálculo de la velocidad y altura para un conjunto de tiempos equiespaciados.
- Los valores de velocidad inicial, altura inicial, valor de gravedad, y número de puntos deben ser argumentos de la función con valores por defecto adecuadamente provistos.
- La tabla de valores debe darse hasta que la partícula toca el piso (valor $h=0$).
- Guarde los resultados en tres columnas (t, v(t), h(t)) en un archivo de nombre “caida_vel_alt.dat”
- donde “vel” corresponde al valor de la velocidad inicial y “alt” al de la altura inicial.
- Realice tres gráficos, mostrando:
  1. altura como función del tiempo (altura en el eje vertical y tiempo en el horizontal)
  2. velocidad como función del tiempo
  3. altura como función de la velocidad
Queremos realizar numéricamente la integral

\[\int_{a}^{b}f(x)dx\]

utilizando el método de los trapecios. Para eso partimos el intervalo $[a,b]$ en $N$ subintervalos y aproximamos la curva en cada subintervalo por una recta

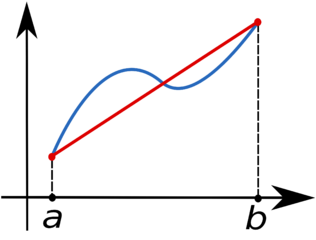
La línea azul representa la función $f(x)$ y la línea roja la interpolación por una recta (figura de https://en.wikipedia.org/wiki/Trapezoidal_rule)

Si llamamos $x_{i}$ ($i=0,\ldots,n,$ con $x_{0}=a$ y $x_{n}=b$) los puntos equiespaciados, entonces queda

\[\int_{a}^{b}f(x)dx\approx\frac{h}{2}\sum_{i=1}^{n}\left(f(x_{i})+f(x_{i-1})\right).\]

En todos los casos utilice arrays y operaciones entre arrays para realizar las siguientes funciones

Escriba una función trapz(x, y) que reciba dos arrays unidimensionales x e y y aplique la fórmula de los trapecios.
Escriba una función trapzf(f, a, b, npts=100) que recibe una función f, los límites a, b y el número de puntos a utilizar npts, y devuelve el valor de la integral por trapecios.
Escriba una función que calcule la integral logarítmica de Euler:

\[\mathrm{Li}(t) = \int_2^t \frac{1}{\ln x} dx\]

usando la función ´trapzf´ para valores de npts=10, 20, 30, 40, 50, 60
Grafique las curvas obtenidas en el punto precedente para valores equiespaciados de $t$ entre 2 y 10.

Vamos a estudiar la frecuencia de aparición de cada dígito en la serie de Fibonacci, generada siguiendo las reglas:

\[a_{1} = a_{2} = 1, \quad a_{i} = a_{i-1} + a_{i-2}.\]

Se pide:
1. Crear una función que acepta como argumento un número entero $N$ y retorna una secuencia (lista, tupla, diccionario o array) con los elementos de la serie de Fibonacci.
2. Crear una función que devuelva un histograma de ocurrencia de cada uno de los dígitos en el primer lugar del número. Por ejemplo para los primeros 8 valores ($N=8$): $1,1,2,3,5,8,13,21$ tendremos que el $1$ aparece 3 veces, el $2$ aparece $2$ veces, $3, 5, 8$ una vez. Normalizar los datos dividiendo por el número de valores $N$.
3. Utilizando las dos funciones anteriores graficar el histograma para un número $N$ grande y comparar los resultados con la ley de Benford
  
  \[P(n) = \log_{10}\left(1+ \frac{1}{d} \right).\]
PARA ENTREGAR: Estimar el valor de π usando diferentes métodos basados en el método de Monte Carlo:
1. Crear una función para calcular el valor de $\pi$ usando el “método de cociente de áreas”. Para ello:
- Generar puntos en el plano dentro del cuadrado de lado unidad cuyo lado inferior va de $x=0$ a $x=1$
- Contar cuantos puntos caen dentro del (cuarto de) círculo unidad. Este número tiende a ser proporcional al área del círculo
- La estimación de $\pi$ será igual a cuatro veces el cociente de números dentro del círculo dividido por el número total de puntos.
1. Crear una función para calcular el valor de $\pi$ usando el “método del valor medio”: Este método se basa en la idea de que el valor medio de una función se puede calcular de dos maneras diferentes. Por un lado es el promedio de los valores de la función si tomamos argumentos al azar en forma aleatoria con una distribución uniforme. Por otro lado, el valor medio verifica la siguiente fórmula integral:
\[\langle f \rangle = \frac{1}{b-a} \int_{a}^{b} f(x)\, dx\]

Tomando la función particular $f(x)= \sqrt{1- x^{2}}$ entre $x=0$ y $x=1$, obtenemos:

\[\langle f \rangle = \int_{0}^{1} \sqrt{1- x^{2}}\, dx = \frac{\pi}{4}\]

Entonces, tenemos que estimar el valor medio de la función $f$ y, mediante la relación entre las dos formas de calcular el valor medio obtener $\pi = 4 \langle f(x) \rangle$.

Para obtener el valor medio de la función tomamos $X$ como una variable aleatoria entre 0 y 1 con distribución uniforme, y el valor promedio de $f(X)$ es justamente $\langle f \rangle$. Su función debe entonces
- Generar puntos aleatoriamente en el intervalo $[0,1]$
- Calcular el valor medio de $f(x)$ para los puntos aleatorios $x$.
- El resultado va a ser igual al valor de la integral, y por lo tanto a $\pi/4$.
1. Utilizar las funciones anteriores con diferentes valores para el número total de puntos $N$. En particular, hacerlo para 20 valores de $N$ equiespaciados logarítmicamente entre 100 y 10000. Para cada valor de $N$ calcular la estimación de $\pi$. Realizar un gráfico con el valor estimado como función del número $N$ con los dos métodos (dos curvas en un solo gráfico)
2. Para $N=15000$ repetir el “experimento” muchas veces (al menos 1000) y realizar un histograma de los valores obtenidos para $\pi$ con cada método. Graficar el histograma y calcular la desviación standard. Superponer una función Gaussiana con el mismo ancho. El gráfico debe ser similar al siguiente (el estilo de graficación no tiene que ser el mismo)
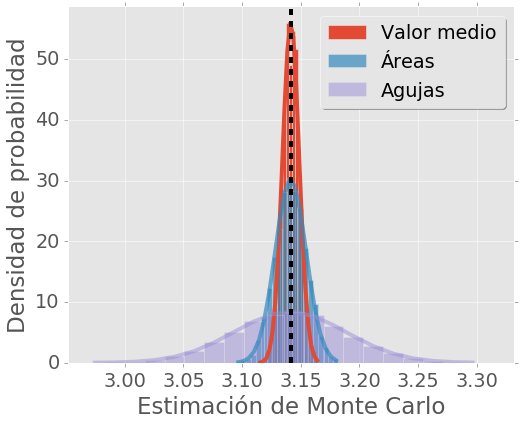
1. El método de la aguja del bufón se puede utilizar para estimar el valor de $\pi$, y consiste en tirar agujas (o palitos, fósforos, etc) al azar sobre una superficie rayada
Por simplicidad vamos a considerar que la distancia entre rayas $t$ es mayor que la longitud de las agujas $\ell$

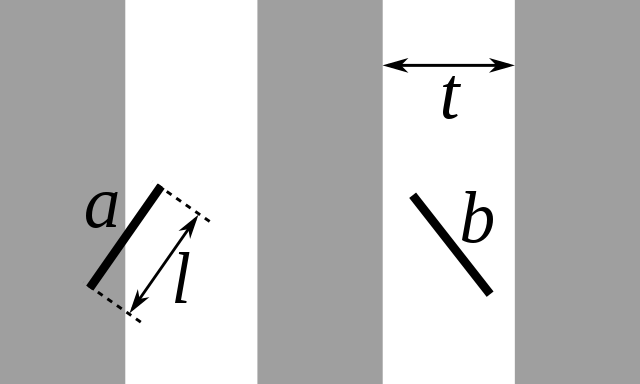
La probabilidad de que una aguja cruce una línea será:

\[P = \frac{2 \ell}{t\, \pi}\]

por lo que podemos calcular el valor de $\pi$ si estimamos la probabilidad $P$. Realizar una función que estime $\pi$ utilizando este método y repetir las comparaciones de los dos puntos anteriores pero ahora utilizando este método y el de las áreas.

Ejercicios de Clase 13

El submódulo scipy.constants tiene valores de constantes físicas de interés. Usando este módulo compute la constante de Stefan-Boltzmann $\sigma$ utilizando la relación:

\[\sigma = \frac{2 \pi^5 k_B^4}{15 h^3 c^2}\]

Confirme que el valor obtenido es correcto comparando con la constante para esta cantidad en scipy.constants
Calcular (utilizando quad) y graficar para valores de $k=1,2,5,10$ como función del límite superior $L$, el valor de las integrales:

\[I_{1}(k,L) = \int_{0}^{L} x^{k} e^{-k x / 2} dx\]

y

\[I_{2}(k,L) = \int_{0}^{L} x^{k} e^{-k x / 2} \sin{(k x)} dx\]

con rango de variación de $L$ entre $0$ y $2 \pi$.

En el archivo co_nrg.dat se encuentran los datos de la posición de los máximos de un espectro de CO2 como función del número cuántico rotacional J (entero). Haga un programa que lea los datos. Los ajuste con polinomios (elija el orden adecuado) y grafique luego los datos (con símbolos) y el ajuste con una línea sólida roja. Además, debe mostrar los parámetros obtenidos para el polinomio.
Para Entregar: Queremos hacer un programa que permita fitear una curva como suma de N funciones gaussianas:
1. Usando distribuciones normales e histogramas cree conjuntos de datos con dos, tres y cuatro máximos.
2. Haga una función, que debe tomar como argumento los arrays con los datos: x, y, y valores iniciales para las Gaussianas: fit_gaussianas(x, y, *params) donde params son los 3N coeficientes (tres coeficientes para cada Gaussiana). Debe devolver los parámetros óptimos obtenidos.
3. Realice un programita que grafique los datos dados y la función que resulta de sumar las gaussianas en una misma figura.
4. Si puede agregue líneas o flechas indicando la posición del máximo y el ancho de cada una de las Gaussianas obtenidas.
Modificar el ejemplo anterior para presentar en una figura tres gráficos, agregando a la izquierda un panel donde se muestre un corte horizontal. El corte debe estar en la mitad del gráfico ($y_{0}=136$). En la figura debe mostrar la posición del corte (similarmente a como se hizo con el corte en $x$) con una línea de otro color.
Dada una imagen en color (por ejemplo, figuras/babbage.png), escribe un programa que calcule y grafique los histogramas de los tres canales de color (rojo, verde y azul) en un único gráfico. Cada canal debe representarse con su color correspondiente.

Ejercicios de Clase 14

Complete la tabla de datos del ejemplo de clase. Para ello utilice el archivo con los pronósticos completos para todas las estaciones, pronostico_5dias20250408.txt y

Agregue una columna con el nombre de la estación al DataFrame
Procese todas las estaciones

Si no lo ha adivinado, los datos de la serie seru corresponden a las edades de los integrantes de la banda Serú Girán, al momento de conformarse, en el año 1978. Encuentre los años de nacimiento de cada uno de sus integrantes.
Una de las funciones más usadas en redes neuronales es softmax, cuyo objetivo es convertir los resultados de las distintas etapas del procesamiento de una red en probabilidades. Los primeros pueden ser números reales de cualquier valor, mientras que las probabilidades deben estar acotadas al intervalo [0,1]. La función softmax aplicada a un conjunto de valores $z_1,\cdots,z_n$ se calcula como

\[\sigma(z_i) = \frac {e^{z_i}} { \sum_{i=1}^n e^{z_i}}\]
- Cree una serie con 10 valores al azar entre 0 y 5
- Obtenga la serie resultante de la aplicación de softmax a la serie anterior

El siguiente es un diccionario que representa el consumo eléctrico mensual de ciertos artefactos eléctricos:

consumo_electrico = {
  "Artefacto": [
     "Heladera", "Lavarropa", "Microondas", "Aire Acondicionado",
     "Televisor", "Computadora", "Lámpara LED", "Secador de Pelo",
     "Horno Eléctrico", "Ventilador"
  ],
  "Consumo Promedio (kWh/mes)": [
     30, 10, 15, 120, 20, 12, 2, 3, 25, 8
  ]
}

Obtenga los tres artefactos de mayor consumo.
Encuentre los artefactos que consumen más de 15 kWH/mes.
Calcule el consumo anual de cada artefacto, y el costo que implica suponiendo que el precio del kWH/mes es de $3145.

Un problema de índices enteros. Supongamos que tenemos la serie
```
s = pd.Series(np.arange(3.0))
```
es decir,
```
0    0.0
1    1.0
2    2.0
dtype: float64
```
¿Cuál es el resultado esperado de s[-1]? ¿Cuál es el real? Evalúe s[-2:-1] y también s.iloc[-1]. Considere ahora la serie
```
s = pd.Series(np.arange(3.0), index=['a','b','c'])
```
y evalúe nuevamente s[-1]. ¿Qué conclusiones puede sacar?
El archivo ‘clima argentina 1981 2010.txt’ contiene datos climáticos significativos de las distintas estaciones meteorológicas del Servicio Meteorológico Nacional.

Inspeccione el archivo y diseñe un tipo DataFrame adecuado para contener dichos datos.
Lea el archivo y cree el DataFrame que diseño en el item anterior.
Cree una función para obtener el promedio anual de las magnitudes climáticas referidas en el archivo. La función debe recibir como argumentos el DataFrame, el nombre de la estación meteorológica y la magnitud, y devolver un valor (float) con el promedio.
Genere un DataFrame que represente todas las magnitudes promedio para cada estación meteorológica, usando la función del item anterior.
Cree funciones para poder realizar gráficos comparativos de los datos meteorológicos. En particular, reproduzca
- El gráfico de Valores Medios de Temperatura y Precipitación
- El gráfico de Valores extremos de Temperatura, usando la temperatura máxima y la mínima de cada mes.

que se pueden ver en el sitio de estadísticas del Servicio Meteorológico Nacional.

Ejercicios de Clase 15

Retome el DataFrame creado en el ejercicio 14(a), y genere un nuevo DataFrame utilizando adecuadamente índices jerárquicos.
En el archivo com3500.csv se encuentra la cotización promedio del dolar en Argentina desde 2002. Lea el archivo en un DataFrame de pandas y

Realice un gráfico claro y bello
Observe que la información del mes está dada en nombre_del_mes-xx donde xx es el año. Separe dicha columna en dos, una correspondiente al mes, y otra correspondiente al año.
Agrupe la información por año y grafique la evolución del precio del dólar por año.