Clase 10: Introducción a Numpy y Matplotlib
Introducción
Dos paquetes que van a resultar muy importantes para nosotros son los
paquetes numpy y matplotlib. Como con todos los módulos, se
cargan utilizando la palabra import, tal como hicimos en los
ejemplos anteriores. Existen variantes en la manera de importar los
módulos que son “equivalentes”. En este caso le vamos a dar un alias que
sea más corto de tipear. Después podemos utilizar sus funciones y
definiciones.
import numpy as np # Importa el paquete numpy para trabajo numérico
import matplotlib.pyplot as plt # Importa el paquete matplotlib para graficación
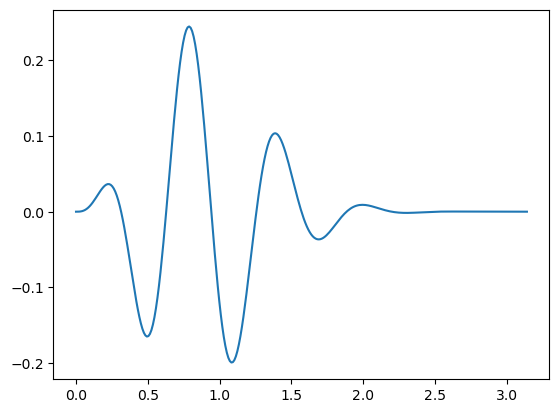
Un ejemplo muy común es la graficación de datos que obtuvimos previamente:
x, y = np.loadtxt('data/ejemplo_plot_07_1.dat', unpack=True)
plt.plot(x, y)
[<matplotlib.lines.Line2D at 0x7fc5903a6ad0>]
Lectura y escritura de datos a archivos
Numpy tiene funciones que permiten escribir y leer datos de varias maneras, tanto en formato texto como en binario. En general el modo texto ocupa más espacio pero puede ser leído y modificado con un editor.
Veamos qué datos hay en el archivo:
Hay dos columnas, en la primera fila hay texto, y en las siguientes hay valores separados por un espacio.
Dos funciones simples y útiles para entrada y salida de datos son
np.loadtxt() para lectura, y np.savetxt() para escritura.
x, y = np.loadtxt('data/ejemplo_plot_07_1.dat', unpack=True)
La función np.loadtxt() carga estos valores a las variables x e
y
len(x), len(y)
(300, 300)
print(x[:10])
[0. 0.010507 0.021014 0.031521 0.042028 0.05253499
0.06304199 0.07354899 0.08405599 0.09456299]
Vemos que, con este uso, la variable x contiene los valores de la
primera columna y la variable y los de la segunda.
Para grabar datos a un archivo le damos como primer argumento el nombre del archivo y como segundo los datos a guardar. Vamos a ver detalles más adelante.
np.savetxt('test.out', y)
!head test.out
0.000000000000000000e+00
1.157617000000000067e-05
9.205286999999999877e-05
3.075649999999999868e-04
7.187931999999999742e-04
1.378427999999999902e-03
2.328857000000000149e-03
3.600144999999999908e-03
5.208355999999999923e-03
7.154281999999999656e-03
En la primera línea hay texto explicativo, en las siguientes líneas el archivo tiene dos columnas.
Veamos que tipo de variable son x e y:
type(x), type(y)
(numpy.ndarray, numpy.ndarray)
Como vemos, el tipo de la variable no es una lista sino un nuevo tipo: ndarray, o simplemente array. Veamos cómo trabajar con ellos.
Características de arrays en Numpy
Numpy define unas nuevas estructuras llamadas ndarrays o arrays para trabajar con vectores de datos, en una dimensión o más dimensiones (“matrices”). Los arrays son variantes de las listas de python preparadas para trabajar a mayor velocidad y menor consumo de memoria. Por ello se requiere que los arrays sean menos generales y versátiles que las listas usuales. Analicemos brevemente las diferencias entre estos tipos y las consecuencias que tendrá en su uso para nosotros.
Comparación de listas y arrays
Comparemos como operamos sobre un conjunto de números cuando los representamos por una lista, o por un array:
dlist = [1.5, 3.8, 4.9, 12.3, 27.2, 35.8, 70.2, 90., 125., 180.]
d = np.array(dlist)
d is dlist
False
print(dlist)
[1.5, 3.8, 4.9, 12.3, 27.2, 35.8, 70.2, 90.0, 125.0, 180.0]
print(d)
[ 1.5 3.8 4.9 12.3 27.2 35.8 70.2 90. 125. 180. ]
type(d), type(dlist)
(numpy.ndarray, list)
Veamos cómo se hace para operar con estos dos tipos. Si los valores representan ángulos en grados, hagamos la conversión a radianes (radián = \(\pi/180\) grado)
2*dlist
[1.5,
3.8,
4.9,
12.3,
27.2,
35.8,
70.2,
90.0,
125.0,
180.0,
1.5,
3.8,
4.9,
12.3,
27.2,
35.8,
70.2,
90.0,
125.0,
180.0]
2*d
array([ 3. , 7.6, 9.8, 24.6, 54.4, 71.6, 140.4, 180. , 250. ,
360. ])
from math import pi
drlist = [a*pi/180 for a in dlist]
print(drlist)
[0.02617993877991494, 0.06632251157578452, 0.08552113334772216, 0.21467549799530256, 0.47472955654245763, 0.62482787221397, 1.2252211349000193, 1.5707963267948966, 2.1816615649929116, 3.141592653589793]
dr = d*(pi/180)
print(dr)
[0.02617994 0.06632251 0.08552113 0.2146755 0.47472956 0.62482787
1.22522113 1.57079633 2.18166156 3.14159265]
Vemos que el modo de trabajar es más simple ya que los array permiten trabajar con operaciones elemento-a-elemento mientras que para las listas tenemos que usar comprensiones de listas. Veamos otros ejemplos:
print([np.sin(a*pi/180) for a in dlist])
[0.02617694830787315, 0.06627390040000014, 0.08541692313736747, 0.21303038627497659, 0.4570979270586942, 0.5849576749872154, 0.9408807689542255, 1.0, 0.819152044288992, 1.2246467991473532e-16]
print(np.sin(np.deg2rad(d)))
[2.61769483e-02 6.62739004e-02 8.54169231e-02 2.13030386e-01
4.57097927e-01 5.84957675e-01 9.40880769e-01 1.00000000e+00
8.19152044e-01 1.22464680e-16]
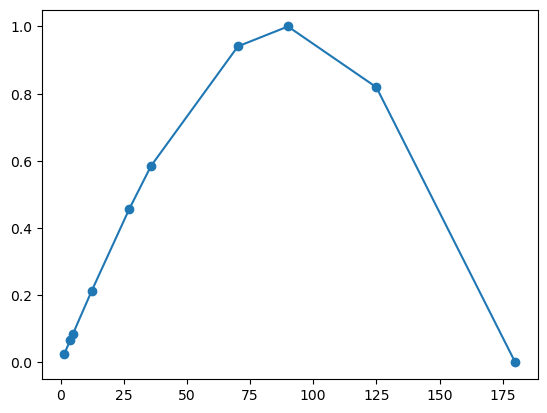
Además de la simplicidad para trabajar con operaciones que actúan sobre
cada elemento, el paquete tiene una gran cantidad de funciones y
constantes definidas (como por ejemplo np.pi para \(\pi\)).
plt.plot(d, np.sin(np.deg2rad(d)),'o-')
plt.show()
Uso de memoria de listas y arrays
Las listas son sucesiones de elementos, completamente generales y no necesariamente todos iguales. Un esquema de su representación interna se muestra en el siguiente gráfico para una lista de números enteros (Las figuras y el análisis de esta sección son de www.python-course.eu/numpy.php)
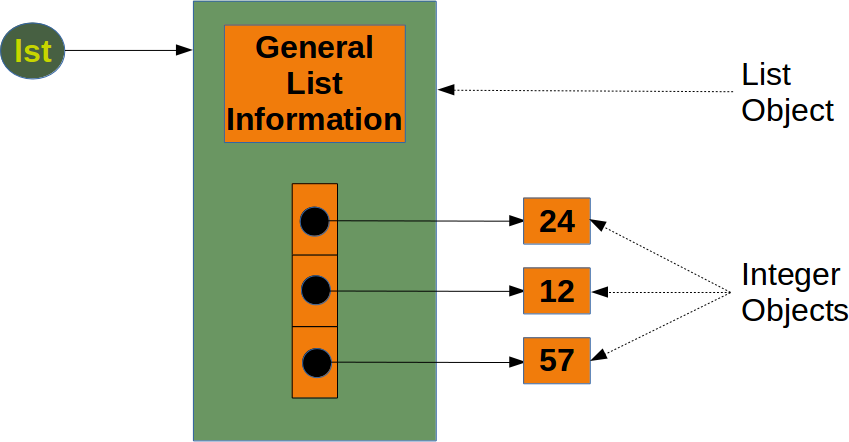
Representación en memoria de una lista
Básicamente en una lista se guarda información común a cualquier lista, un lugar de almacenamiento que referencia donde buscar cada uno de sus elementos (que puede ser un objeto diferente) y luego el lugar efectivo para guardar cada elemento. Veamos cuanta memoria se necesita para guardar una lista de enteros:
from sys import getsizeof
lst = [24, 12, 57]
size_of_list_object = getsizeof(lst) # La lista sin sus datos
#size_of_elements = getsizeof(lst[0]) + getsizeof(lst[1]) + getsizeof(lst[2])
size_of_elements = sum(getsizeof(l) for l in lst)
total_list_size = size_of_list_object + size_of_elements
print("Tamaño sin considerar los elementos: ", size_of_list_object)
print("Tamaño de los elementos: ", size_of_elements)
print("Tamaño total: ", total_list_size)
Tamaño sin considerar los elementos: 88
Tamaño de los elementos: 84
Tamaño total: 172
Para calcular cuánta memoria se usa en cada parte de una lista analicemos el tamaño de distintos casos:
print('Una lista vacía ocupa: {} bytes'.format(getsizeof([])))
print('Una lista con un elem: {} bytes'.format(getsizeof([24])))
print('Una lista con 2 elems: {} bytes'.format(getsizeof([24,12])))
print('Un entero en Python : {} bytes'.format(getsizeof(24)))
Una lista vacía ocupa: 56 bytes
Una lista con un elem: 64 bytes
Una lista con 2 elems: 72 bytes
Un entero en Python : 28 bytes
Vemos que la “Información general de listas” ocupa 56 bytes, y la referencia a cada elemento entero ocupa adicionalmente 8 bytes, por lo que la lista con dos elementos ocupa 72 bytes. Además, cada elemento, un entero de Python, en este caso ocupa 28 bytes, por lo que el tamaño total de una lista de \(n\) números enteros será:
En contraste, los arrays deben ser todos del mismo tipo por lo que su representación es más simple (por ejemplo, no es necesario guardar sus valores separadamente)

Representación en memoria de una lista
a = np.array(lst, dtype='int')
print(getsizeof(a))
136
Para analizar como se distribuye el consumo de memoria en un array vamos a calcular el tamaño de cada uno de los elementos como hicimos con las listas:
print('Un array vacío ocupa: {} bytes'.format(getsizeof(np.array([]))))
print('Un array con un elem: {} bytes'.format(getsizeof(np.array([24]))))
print('Un array con 2 elems: {} bytes'.format(getsizeof(np.array([24,12]))))
print('Un entero de Numpy es: {}'.format(type(a[0])))
print('Un entero de Numpy usa: {}'.format(getsizeof(a[0])))
Un array vacío ocupa: 112 bytes
Un array con un elem: 120 bytes
Un array con 2 elems: 128 bytes
Un entero de Numpy es: <class 'numpy.int64'>
Un entero de Numpy usa: 32
Vemos que la información general sobre arrays ocupa 96 bytes (en
contraste a 64 para listas), y por cada elemento otros 8 bytes
adicionales (numpy.int64 corresponde a 64 bits), por lo que el
tamaño total será:
from sys import getsizeof
lst1 = list(range(50000))
total_list_size = getsizeof(lst1) + sum(getsizeof(l) for l in lst1)
print("Tamaño total de la lista: ", total_list_size)
a1 = np.array(lst1)
print("Tamaño total de array: ", getsizeof(a1))
Tamaño total de la lista: 1800056
Tamaño total de array: 400112
Velocidad de Numpy
Una de las grandes ventajas de usar Numpy está relacionada con la velocidad de cálculo. Veamos (superficialmente) esto
# %load scripts/timing.py
# Ejemplo del libro en www.python-course.eu/numpy.php
import numpy as np
from timeit import Timer
Ndim = 200000
def pure_python_version():
X = range(Ndim)
Y = range(Ndim)
Z = []
for i in range(len(X)):
Z.append(X[i] + Y[i])
return Z
def numpy_version():
X = np.arange(Ndim)
Y = np.arange(Ndim)
Z = X + Y
return Z
timer_obj1 = Timer("pure_python_version()", "from __main__ import pure_python_version")
timer_obj2 = Timer("numpy_version()", "from __main__ import numpy_version")
t1 = timer_obj1.timeit(10)
t2 = timer_obj2.timeit(10)
print(f"Numpy es en este ejemplo {t1 / t2 : .3f} más rápido")
Numpy es en este ejemplo 93.568 más rápido
Como vemos, utilizar Numpy puede ser considerablemente más rápido que usar Python puro.
Propiedades de Numpy arrays
Hay tres propiedades básicas que caracterizan a un array:
shape: Contiene información sobre la forma que tiene un array (sus dimensiones: vector, matriz, o tensor)dtype: Es el tipo de cada uno de sus elementos (todos son iguales)stride: Contiene la información sobre como recorrer el array. Por ejemplo si es una matriz, tiene la información de cuántos bytes en memoria hay que pasar para pasar de una fila a la siguiente y de una columna a la siguiente.
arr = np.array([[1,2,3], [4,5,6]])
print( 'shape :', arr.shape)
print( 'dtype :', arr.dtype)
print( 'strides:', arr.strides)
shape : (2, 3)
dtype : int64
strides: (24, 8)
print(arr)
[[1 2 3]
[4 5 6]]
arr[1,0]
4
Los array tienen otros atributos que nos dan información sobre sus
características, por ejemplo size y ndim que nos dan el tamaño
total y el número de dimensiones:
print( 'Número total de elementos :', arr.size)
print( 'Número de dimensiones :', arr.ndim)
Número total de elementos : 6
Número de dimensiones : 2
Creación de arrays en Numpy
Un array en numpy es un tipo de variable parecido a una lista, pero
está optimizado para realizar trabajo numérico.
Todos los elementos deben ser del mismo tipo, y además de los valores, contiene información sobre su tipo. Veamos algunos ejemplos de cómo crearlos y utilizarlos:
Creación de Arrays unidimensionales
i1 = np.array([1, 2, 3, 1, 5, 1, 9, 22, 0])
r1 = np.array([1.4 ,2.3 ,3.0 ,1, 5, 1, 9, 22, 0])
print(i1)
print(r1)
[ 1 2 3 1 5 1 9 22 0]
[ 1.4 2.3 3. 1. 5. 1. 9. 22. 0. ]
print(f"tipo de i1: {i1.dtype} \ntipo de r1: {r1.dtype}")
tipo de i1: int64
tipo de r1: float64
print(f"Para i1:\n Número de dimensiones: {np.ndim(i1)}\n Longitud: {len(i1)}")
Para i1:
Número de dimensiones: 1
Longitud: 9
print(f"Para r1:\n Número de dimensiones: {r1.ndim}\n Longitud: {len(r1)}")
Para r1:
Número de dimensiones: 1
Longitud: 9
Arrays multidimensionales
Podemos crear explícitamente arrays multidimensionales con la función
np.array si el argumento es una lista anidada
L = [ [1, 2, 3], [.2, -.2, -1], [-1, 2, 9], [0, 0.5, 0] ]
A = np.array(L)
A
array([[ 1. , 2. , 3. ],
[ 0.2, -0.2, -1. ],
[-1. , 2. , 9. ],
[ 0. , 0.5, 0. ]])
print(A)
[[ 1. 2. 3. ]
[ 0.2 -0.2 -1. ]
[-1. 2. 9. ]
[ 0. 0.5 0. ]]
print(np.ndim(A), A.ndim) # Ambos son equivalentes
2 2
print(len(A))
4
Vemos que la dimensión de A es 2, pero la longitud que me reporta
Python corresponde al primer eje. Los arrays tienen un atributo
que es la “forma” (shape)
print(A.shape)
(4, 3)
r1.shape # una tupla de un solo elemento
(9,)
Generación de datos equiespaciados
Para obtener datos equiespaciados hay dos funciones complementarias
a1 = np.arange(0,190,10)
a2 = np.linspace(0,180,19)
a1
array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120,
130, 140, 150, 160, 170, 180])
a2
array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90., 100.,
110., 120., 130., 140., 150., 160., 170., 180.])
Como vemos, ambos pueden dar resultados similares, y es una cuestión de conveniencia cual utilizar. El uso es:
np.arange([start,] stop[, step,], dtype=None)
np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
Mientras que a arange() le decimos cuál es el paso a utilizar, a
linspace() debemos (podemos) darle como tercer argumento el número
de valores que queremos.
# Si queremos que devuelva enteros:
np.arange(0,180.,7.8)
array([ 0. , 7.8, 15.6, 23.4, 31.2, 39. , 46.8, 54.6, 62.4,
70.2, 78. , 85.8, 93.6, 101.4, 109.2, 117. , 124.8, 132.6,
140.4, 148.2, 156. , 163.8, 171.6, 179.4])
# Si queremos que devuelva enteros:
np.arange(0,180.,7.8, dtype=int)
array([ 0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84,
91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161])
# Pedimos que devuelva el paso también
v1, step1 = np.linspace(0,10,20, endpoint=True, retstep=True)
v2, step2 = np.linspace(0,10,20, endpoint=False, retstep=True)
print(step1)
print(step2)
0.5263157894736842
0.5
v1
array([ 0. , 0.52631579, 1.05263158, 1.57894737, 2.10526316,
2.63157895, 3.15789474, 3.68421053, 4.21052632, 4.73684211,
5.26315789, 5.78947368, 6.31578947, 6.84210526, 7.36842105,
7.89473684, 8.42105263, 8.94736842, 9.47368421, 10. ])
v2
array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. ,
6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])
plt.plot(a2, np.sin(np.deg2rad(a2)),'o-')
plt.show()
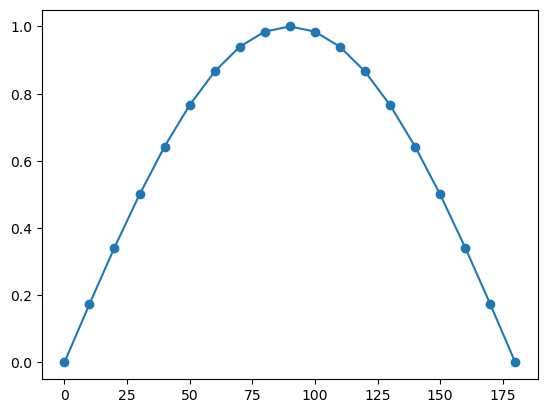
Además de valores linealmente espaciados podemos obtener valores espaciados en escala logarítmica
w = np.logspace(0,10,10)
plt.plot( w, 'o-')
plt.show()
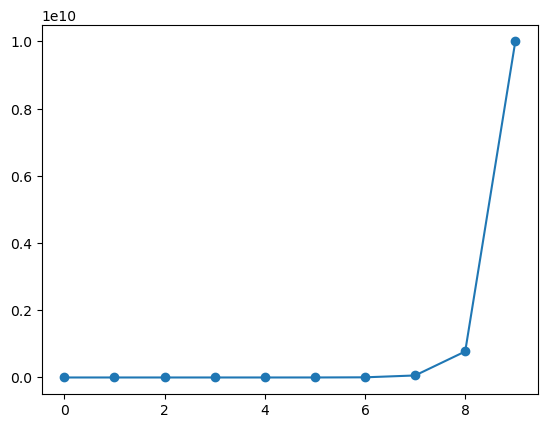
w1 = np.logspace(0,2,3) # Start y Stop son los exponentes
print(w1)
[ 1. 10. 100.]
w2 = np.geomspace(1,100,3) # Start y Stop son los valores
print(w2)
[ 1. 10. 100.]
Otras formas de creación
Hay otras maneras de crear numpy arrays. Algunas, de las más comunes es cuando necesitamos crear un array con todos ceros o unos o algún valor dado
a = np.zeros(5)
a.dtype # El tipo default es float de 64 bits
dtype('float64')
print(a)
[0. 0. 0. 0. 0.]
i= np.zeros(5, dtype=int)
print(i)
[0 0 0 0 0]
i.dtype
dtype('int64')
c = np.zeros(5,dtype=complex)
print(c)
print(c.dtype)
[0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
complex128
En lugar de inicializarlo en cero podemos inicializarlo con algún valor
np.ones(5, dtype=complex) # Algo similar pero inicializando a unos
array([1.+0.j, 1.+0.j, 1.+0.j, 1.+0.j, 1.+0.j])
Ya vimos que también podemos inicializarlos con valores “equiespaciados”
con np.arange(), con np.linspace() o con np.logspace()
v = np.arange(2,15,2) # Crea un array con una secuencia (similar a la función range)
Para crear arrays multidimensionales usamos:
np.ones((4,5))
array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
np.ones((4,3,6))
array([[[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]]])
np.eye(4)
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
np.eye(3,7)
array([[1., 0., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0., 0.]])
En este último ejemplo hemos creado matrices con unos en la diagonal y ceros en todos los demás lugares.
Acceso a los elementos
El acceso a los elementos tiene una forma muy parecida a la de las listas (pero no exactamente igual).
print(r1)
[ 1.4 2.3 3. 1. 5. 1. 9. 22. 0. ]
Si queremos uno de los elementos usamos la notación:
print(r1[0], r1[3], r1[-1])
1.4 1.0 0.0
y para “tajadas” (slices)
print(r1[:3])
[1.4 2.3 3. ]
print(r1[-3:])
[ 9. 22. 0.]
print(r1[5:7])
[1. 9.]
print(r1[0:8:2])
[1.4 3. 5. 9. ]
Como con vectores unidimensionales, con arrays multidimensionales, se puede ubicar un elemento o usar slices:
X = np.arange(55).reshape((5,11))
X
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21],
[22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32],
[33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43],
[44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54]])
print("primer y segundo elementos", X[0,0], X[0,1])
primer y segundo elementos 0 1
print( 'Slicing parte de la segunda fila :', X[1, 2:4])
print('Todas las filas, tercera columna :', X[:, 2])
Slicing parte de la segunda fila : [13 14]
Todas las filas, tercera columna : [ 2 13 24 35 46]
print( 'Primera fila :\n', X[0], '\nes igual a :\n', X[0,:])
Primera fila :
[ 0 1 2 3 4 5 6 7 8 9 10]
es igual a :
[ 0 1 2 3 4 5 6 7 8 9 10]
print( 'Segunda fila :\n', X[1], '\nes igual a :\n', X[1,:])
Segunda fila :
[11 12 13 14 15 16 17 18 19 20 21]
es igual a :
[11 12 13 14 15 16 17 18 19 20 21]
print( 'Primera columna:', X[:,0])
Primera columna: [ 0 11 22 33 44]
print( 'Última columna : \n', X[:,-1])
Última columna :
[10 21 32 43 54]
print( 'Segunda fila, elementos impares (0,2,...) : ', X[1,::2])
Segunda fila, elementos impares (0,2,...) : [11 13 15 17 19 21]
print( 'Segunda fila, todos los elementos pares : ', X[1,1::2])
Segunda fila, todos los elementos pares : [12 14 16 18 20]
Cuando el slicing se hace de la forma [i:f:s] significa que
tomaremos los elementos entre i (inicial), hasta f (final, no
incluido), pero tomando sólo uno de cada s (stride) elementos
X[2:,3:5]
array([[25, 26],
[36, 37],
[47, 48]])
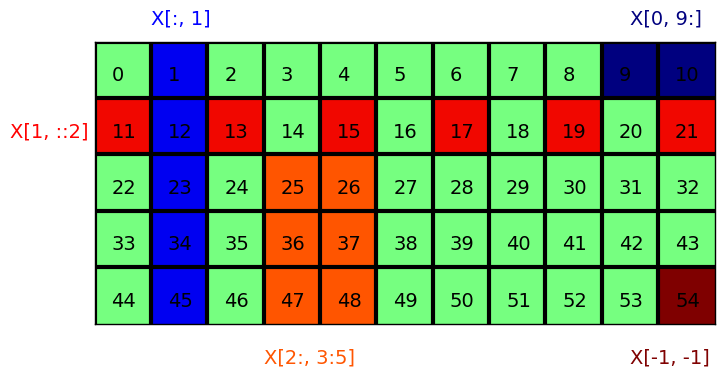
En Scipy Lectures at http://scipy-lectures.github.io hay una descripción del acceso a arrays.
Operaciones sobre arrays
Operaciones básicas
Los array se pueden usar en operaciones:
arr = np.linspace(1,10,10)+ 1
arr
array([ 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])
# Suma de una constante
arr1 = 2* arr[::-1] # Creamos un segundo array
arr[::-1]
array([11., 10., 9., 8., 7., 6., 5., 4., 3., 2.])
arr1
array([22., 20., 18., 16., 14., 12., 10., 8., 6., 4.])
# Multiplicación y división por constantes y suma/resta de arrays
2*arr1 - arr/2
array([43. , 38.5, 34. , 29.5, 25. , 20.5, 16. , 11.5, 7. , 2.5])
# Multiplicación entre arrays
arr * arr1
array([44., 60., 72., 80., 84., 84., 80., 72., 60., 44.])
arr / arr1
array([0.09090909, 0.15 , 0.22222222, 0.3125 , 0.42857143,
0.58333333, 0.8 , 1.125 , 1.66666667, 2.75 ])
Como vemos, están definidas todas las operaciones por constantes y entre arrays. En operaciones con constantes, se aplican sobre cada elemento del array. En operaciones entre arrays se realizan elemento a elemento (y el número de elementos de los dos array debe ser compatible).
Comparaciones
También se pueden comparar dos arrays elemento a elemento
v = np.linspace(0,19,20)
w = np.linspace(0.5,18,20)
print (v)
print (w)
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.
18. 19.]
[ 0.5 1.42105263 2.34210526 3.26315789 4.18421053 5.10526316
6.02631579 6.94736842 7.86842105 8.78947368 9.71052632 10.63157895
11.55263158 12.47368421 13.39473684 14.31578947 15.23684211 16.15789474
17.07894737 18. ]
# Comparación de un array con una constante
print(v > 12)
[False False False False False False False False False False False False
False True True True True True True True]
# Comparación de un array con otro
print(v > w)
[False False False False False False False True True True True True
True True True True True True True True]
Funciones definidas en Numpy
Algunas de las funciones definidas en numpy se aplican a cada elemento. Por ejemplo, las funciones matemáticas:
np.sin(arr1)
array([-0.00885131, 0.91294525, -0.75098725, -0.28790332, 0.99060736,
-0.53657292, -0.54402111, 0.98935825, -0.2794155 , -0.7568025 ])
np.exp(-arr**2/2)
array([1.35335283e-01, 1.11089965e-02, 3.35462628e-04, 3.72665317e-06,
1.52299797e-08, 2.28973485e-11, 1.26641655e-14, 2.57675711e-18,
1.92874985e-22, 5.31109225e-27])
Ejercicios 10 (a)
Genere arrays en 2d, cada uno de tamaño 10x10 con:
Un array con valores 1 en la “diagonal principal” y 0 en el resto (Matriz identidad).
Un array con valores 0 en la “diagonal principal” y 1 en el resto.
Un array con valores 1 en los bordes y 0 en el interior.
Un array con números enteros consecutivos (empezando en 1) en los bordes y 0 en el interior.
Diga qué resultado produce el siguiente código, y explíquelo
# Ejemplo propuesto por Jake VanderPlas
print(sum(range(5),-1))
from numpy import *
print(sum(range(5),-1))
Escriba una función
suma_potencias(p, n)(utilizando arrays y Numpy) que calcule la operación\[s_{2} = \sum_{k=0}^{n}k^{p}\].
Usando las funciones de numpy
signymaximumdefinir las siguientes funciones, que acepten como argumento un array y devuelvan un array con el mismo shape:
función de Heaviside, que vale 1 para valores positivos de su argumento y 0 para valores negativos.
La función escalón, que vale 0 para valores del argumento fuera del intervalo \((-1,1)\) y 1 para argumentos en el intervalo.
La función rampa, que vale 0 para valores negativos de \(x\) y \(x\) para valores positivos.