Clase 5: Más características de Funciones
Empacar y desempacar argumentos
Cuando en Python creamos una función que acepta un número arbitrario de argumentos estamos utilizando una habilidad del lenguaje que es el “empaquetamiento” y “desempaquetamiento” automático de variables.
Al definir un número variable de argumentos de la forma:
def f(*v):
...
y luego utilizarla en alguna de las formas:
f(1)
f(1,'hola')
f(a,2,3.5, 'hola')
Python automáticamente convierte los argumentos en una única tupla:
f(1) --> v = (1,)
f(1,'hola') --> v = (1,'hola')
f(a,2,3.5, 'hola') --> v = (a,2,3.5,'hola')
Análogamente, cuando utilizamos funciones podemos desempacar múltiples valores en los argumentos de llamada a las funciones.
Si definimos una función que recibe un número determinado de argumentos
def g(a, b, c):
...
y definimos una lista (o tupla)
t1 = [a1, b1, c1]
podemos realizar la llamada a la función utilizando la notación “asterisco” o “estrella”
g(*t1) --> g(a1, b1, c1)
Esta notación no se puede utilizar en cualquier contexto. Por ejemplo, es un error tratar de hacer
t2 = *t1
pero en el contexto de funciones podemos “desempacarlos” para
convertirlos en varios argumentos que acepta la función usando la
expresión con asterisco. Veamos lo que esto quiere decir con la función
caida_libre() definida anteriormente
def caida_libre(t, h0, v0 = 0., g=9.8):
"""Devuelve la velocidad y la posición de una partícula en
caída libre para condiciones iniciales dadas
Parameters
----------
t : float
el tiempo al que queremos realizar el cálculo
h0: float
la altura inicial
v0: float (opcional)
la velocidad inicial (default = 0.0)
g: float (opcional)
valor de la aceleración de la gravedad (default = 9.8)
Returns
-------
(v,h): tuple of floats
v= v0 - g*t
h= h0 - v0*t -g*t^2/2
"""
v = v0 - g*t
h = h0 - v0*t - g*t**2/2.
return v,h
datos = (5.4, 1000., 0.) # Una lista (tuple en realidad)
# print (caida_libre(datos[0], datos[1], datos[2]))
print (caida_libre(*datos))
(-52.92000000000001, 857.116)
En la llamada a la función, la expresión *datos le indica al
intérprete Python que la secuencia (tuple) debe convertirse en una
sucesión de argumentos, que es lo que acepta la función.
Similarmente, para desempacar un diccionario usamos la notación
**diccionario:
# diccionario, caída libre en la luna
otros_datos = {'t':5.4, 'h0': 1000., "g" : 1.625}
v, h = caida_libre(**otros_datos)
print ('v={}, h={}'.format(v,h))
v=-8.775, h=976.3075
En resumen:
la notación
(*datos)convierte la tupla (o lista) en los tres argumentos que acepta la función caída libre. Los siguientes llamados son equivalentes:
caida_libre(*datos)
caida_libre(datos[0], datos[1], datos[2])
caida_libre(5.4, 1000., 0.)
la notación
(**otros_datos)desempaca el diccionario en paresclave=valor, siendo equivalentes los dos llamados:
caida_libre(**otros_datos)
caida_libre(t=5.4, h0=1000., g=0.2)
Funciones que devuelven funciones
Las funciones pueden ser pasadas como argumento y pueden ser retornadas por una función, como cualquier otro objeto (números, listas, tuples, cadenas de caracteres, diccionarios, etc). Veamos un ejemplo simple de funciones que devuelven una función:
def crear_potencia(n):
"Devuelve la función x^n"
def potencia(x):
"potencia {}-esima de x".format(n)
return x**n
return potencia
f = crear_potencia(3) # f = x^3
print(f)
cubos = [f(j) for j in range(5)]
<function crear_potencia.<locals>.potencia at 0x7f4126ec8180>
cubos
[0, 1, 8, 27, 64]
help(f)
Help on function potencia in module __main__:
potencia(x)
help(crear_potencia)
Help on function crear_potencia in module __main__:
crear_potencia(n)
Devuelve la función x^n
Ejemplo: Polinomio interpolador
Veamos ahora una función que retorna una función. Supongamos que tenemos
una tabla de puntos (x,y) por los que pasan nuestros datos y
queremos interpolar los datos con un polinomio.
Sabemos que dados M-1 puntos, hay un único polinomio de grado
M-1 que pasa por todos los puntos. En este ejemplo utilizamos la
fórmula de Lagrange para obtenerlo.
def polinomio_interp(x, y):
"""Devuelve el polinomio interpolador que pasa por los puntos (x_i, y_i)
Warning: La implementación es numéricamente inestable. Funciona para algunos puntos (menor a 20)
Keyword Arguments:
x -- Lista con los valores de x
y -- Lista con los valores de y
"""
M = len(x)
def polin(xx):
"""Evalúa el polinomio interpolador de Lagrange"""
P = 0
for j in range(M):
pt = y[j]
# Cálculo de l_
for k in range(M):
if k == j:
continue
fac = x[j] - x[k]
pt *= (xx - x[k]) / fac
P += pt
return P
return polin
Lo que obtenemos al llamar a esta función es una función
f = polinomio_interp([0,1], [0,2])
f
<function __main__.polinomio_interp.<locals>.polin(xx)>
help(f)
Help on function polin in module __main__:
polin(xx)
Evalúa el polinomio interpolador de Lagrange
f(3.4)
6.8
Este es el resultado esperado porque queremos el polinomio que pasa por dos puntos (una recta), y en este caso es la recta \(y = 2x\). Veamos cómo usarlo, en forma más general:
xmax = 5
step = 0.2
N = int(5 / step)
x2, y2 = [1, 2, 3], [1, 4, 9] # x^2
f2 = polinomio_interp(x2, y2)
x3, y3 = [0, 1, 2, 3], [0, 2, 16, 54] # 2 x^3
f3 = polinomio_interp(x3, y3)
print('\n x f2(x) f3(x)\n' + 18 * '-')
for j in range(N):
x = step * j
print(f'{x:.1f} {f2(x):5.2f} {f3(x):6.2f}')
x f2(x) f3(x)
------------------
0.0 0.00 0.00
0.2 0.04 0.02
0.4 0.16 0.13
0.6 0.36 0.43
0.8 0.64 1.02
1.0 1.00 2.00
1.2 1.44 3.46
1.4 1.96 5.49
1.6 2.56 8.19
1.8 3.24 11.66
2.0 4.00 16.00
2.2 4.84 21.30
2.4 5.76 27.65
2.6 6.76 35.15
2.8 7.84 43.90
3.0 9.00 54.00
3.2 10.24 65.54
3.4 11.56 78.61
3.6 12.96 93.31
3.8 14.44 109.74
4.0 16.00 128.00
4.2 17.64 148.18
4.4 19.36 170.37
4.6 21.16 194.67
4.8 23.04 221.18
Ejercicios 05 (a)
Escriba una función
crear_sen(A, w)que acepte dos números reales \(A, w\) como argumentos y devuelva la funciónf(x).
Al evaluar la función f en un dado valor \(x\) debe dar el
resultado: \(f(x) = A \sin(w x)\) tal que se pueda utilizar de la
siguiente manera:
from math import pi
f = crear_sen(3, 2)
f(pi/2)
# Debería imprimir el resultado de 3*sin(2 * pi/2) aprox. cero
Funciones que toman como argumento una función
def aplicar_fun(f, L):
"""Aplica la función f a cada elemento del iterable L
devuelve una lista con los resultados.
IMPORTANTE: Notar que no se realiza ninguna comprobación de validez
"""
return [f(x) for x in L]
En lenguajes funcionales la función ``aplicar_fun`` se llama *map*
import math as m
Lista = list(range(1,10))
t = aplicar_fun(m.sin, Lista)
t
[0.8414709848078965,
0.9092974268256817,
0.1411200080598672,
-0.7568024953079282,
-0.9589242746631385,
-0.27941549819892586,
0.6569865987187891,
0.9893582466233818,
0.4121184852417566]
Notar que definimos la función aplicar_fun() que recibe una función
y una secuencia, pero no necesariamente una lista, por lo que podemos
aplicarla directamente a range:
aplicar_fun(crear_potencia(3), range(5))
[0, 1, 8, 27, 64]
Además, debido a su definición, el primer argumento de la función
aplicar_fun() no está restringida a funciones numéricas pero al
usarla tenemos que asegurar que la función y el iterable (lista) que
pasamos como argumentos son compatibles.
Veamos otro ejemplo:
s = ['hola', 'chau']
print(aplicar_fun(str.upper, s))
['HOLA', 'CHAU']
donde str.upper es una función definida en Python, que convierte
a mayúsculas el string dado str.upper('hola') = 'HOLA'.
Aplicacion: Ordenamiento de listas
Consideremos el problema del ordenamiento de una lista de strings. Como vemos el resultado usual no es necesariamente el deseado
s1 = ['Estudiantes', 'caballeros', 'Python', 'Curso', 'pc', 'aereo']
print(s1)
print(sorted(s1))
['Estudiantes', 'caballeros', 'Python', 'Curso', 'pc', 'aereo']
['Curso', 'Estudiantes', 'Python', 'aereo', 'caballeros', 'pc']
Acá sorted es una función, similar al método str.sort() que
mencionamos anteriormente, con la diferencia que devuelve una nueva
lista con los elementos ordenados. Como los elementos son strings, la
comparación se hace respecto a su posición en el abecedario. En este
caso no es lo mismo mayúsculas o minúsculas.
s2 = [s.lower() for s in s1]
print(s2)
print(sorted(s2))
['estudiantes', 'caballeros', 'python', 'curso', 'pc', 'aereo']
['aereo', 'caballeros', 'curso', 'estudiantes', 'pc', 'python']
Posiblemente queremos el orden que obtuvimos en segundo lugar pero con
los elementos dados originalmente (con sus mayúsculas y minúsculas
originales). Para poder modificar el modo en que se ordenan los
elementos, la función sorted (y el método sort) tienen el
argumento opcional key que debe ser una función. Entonces sort()
y sorted() toman una función como argumento.
sorted(s1, key=str.lower)
['aereo', 'caballeros', 'Curso', 'Estudiantes', 'pc', 'Python']
Como vemos, los strings están ordenados adecuadamente. Si queremos ordenarlos por longitud de la palabra
sorted(s1, key=len)
['pc', 'Curso', 'aereo', 'Python', 'caballeros', 'Estudiantes']
Supongamos que queremos ordenarla alfabéticamente por la segunda letra
def segunda(a):
return a[1]
sorted(s1, key=segunda)
['caballeros', 'pc', 'aereo', 'Estudiantes', 'Curso', 'Python']
Funciones anónimas
En ocasiones como esta suele ser más rápido (o conveniente) definir la función, que se va a utilizar una única vez, sin darle un nombre. Estas se llaman funciones lambda, y el ejemplo anterior se escribiría
sorted(s1, key=lambda a: a[1])
['caballeros', 'pc', 'aereo', 'Estudiantes', 'Curso', 'Python']
Si queremos ordenarla alfabéticamente empezando desde la última letra:
sorted(s1, key=lambda a: str.lower(a[::-1]))
['pc', 'Python', 'aereo', 'Curso', 'Estudiantes', 'caballeros']
Este es un ejemplo de uso de las funciones anónimas lambda. La forma
general de las funciones lambda es:
lambda x,y,z: expresión_de(x,y,z)
por ejemplo, para calcular \((n+1) x^n\), hicimos:
lambda x,n: (n+1) * x**n
Ejemplo: Integración numérica
Veamos en más detalle el caso de funciones que reciben como argumento otra función, estudiando un caso usual: una función de integración debe recibir como argumento al menos una función a integrar y los límites de integración:
En este ejemplo programamos la fórmula de integración de Simpson para
obtener la integral de una función f(x) provista por el usuario, en
un dado intervalo:
def integrate_simps(f, a, b, N=10):
"""Calcula numéricamente la integral de la función en el intervalo dado
utilizando la regla de Simpson
Keyword Arguments:
f -- Función a integrar
a -- Límite inferior
b -- Límite superior
N -- El intervalo se separa en 2*N intervalos
"""
h = (b - a) / (2 * N)
I = f(a) - f(b)
for j in range(1, N + 1):
x2j = a + 2 * j * h
x2jm1 = a + (2 * j - 1) * h
I += 2 * f(x2j) + 4 * f(x2jm1)
return I * h / 3
¿Cómo usamos la función de integración?
def potencia2(x):
return x**2
integrate_simps(potencia2, 0, 3, 7)
9.0
Acá definimos una función, y se la pasamos como argumento a la función de integración.
Uso de funciones anónimas
Veamos como sería el uso de funciones anónimas en este contexto
integrate_simps(lambda x: x**2, 0, 3, 7)
9.0
La notación es un poco más corta, que es cómodo pero no muy relevante para un caso. Si queremos, por ejemplo, aplicar el integrador a una familia de funciones la notación se simplifica notablemente:
print('Integrales:')
a = 0
b = 3
for n in range(6):
I = integrate_simps(lambda x: (n + 1) * x**n, a, b, 10)
print(f'I ( {n+1} x^{n}, {a}, {b} ) = {I:.5f}')
Integrales:
I ( 1 x^0, 0, 3 ) = 3.00000
I ( 2 x^1, 0, 3 ) = 9.00000
I ( 3 x^2, 0, 3 ) = 27.00000
I ( 4 x^3, 0, 3 ) = 81.00000
I ( 5 x^4, 0, 3 ) = 243.00101
I ( 6 x^5, 0, 3 ) = 729.00911
Ejercicios 05 (b)
Escriba una serie de funciones que permitan trabajar con polinomios. Vamos a representar a un polinomio como una lista de números reales, donde cada elemento corresponde a un coeficiente que acompaña una potencia. En cada caso elija los argumentos que considere necesario.
Una función que devuelva el orden del polinomio (un número entero)
Una función que sume dos polinomios y devuelva un polinomio (objeto del mismo tipo)
Una función que multiplique dos polinomios y devuelva el resultado en otro polinomio
Una función devuelva la derivada del polinomio (otro polinomio).
Una función que acepte el polinomio y devuelva la función correspondiente.
Escriba una función
direccion_media(ang1, ang2, ...)cuyos argumentos son direcciones en el plano, expresadas por los ángulos en grados a partir de un cierto eje, y calcule la dirección promedio, expresada en ángulos. Pruebe su función con las listas:a1 = direccion_media(0, 180, 370, 10) a2 = direccion_media(30, 0, 80, 180) a3 = direccion_media(80, 180, 540, 280)
Las funciones de Bessel de orden \(n\) cumplen las relaciones de recurrencia
\[J_{n -1}(x)- \frac{2n }{x}\, J_{n }(x) + J_{n +1}(x) = 0\]\[J^{2}_{0}(x) + \sum_{n=1}^{\infty} 2 J^{2}_{n}(x) = 1\]Para calcular la función de Bessel de orden \(N\), se empieza con un valor de \(M \gg N\), y utilizando los valores iniciales \(J_{M}=1\), \(J_{M+1}=0\) se utiliza la primera relación para calcular todos los valores de \(n < M\). Luego, utilizando la segunda relación se normalizan todos los valores.
Nota
Estas relaciones son válidas si \(M \gg x\) (use algún valor estimado, como por ejemplo \(M=N+20\)).
Utilice estas relaciones para calcular \(J_{N}(x)\) para \(N=3,4,7\) y \(x=2.5, 5.7, 10\). Para referencia se dan los valores esperados
\[\begin{split}\begin{align} J_3( 2.5) = 0.21660\\ J_4( 2.5) = 0.07378\\ J_7( 2.5) = 0.00078\\ J_3( 5.7) = 0.20228\\ J_4( 5.7) = 0.38659\\ J_7( 5.7) = 0.10270\\ J_3(10.0) = 0.05838\\ J_4(10.0) = -0.21960\\ J_7(10.0) = 0.21671\\ \end{align}\end{split}\]Dada una lista de números, vamos a calcular valores relacionados a su estadística.
Realizar una función
calc_media(x, que="aritmetica")que calcule los valores de la media aritmética, la media geométrica o la media armónica dependiendo del valor del argumentoque. Las medias están dadas por:\[A(x_1, \ldots, x_n) = \bar{x} = \frac{x_1 + \cdots + x_n}{n}\]\[G(x_1, \ldots, x_n) = \sqrt[n]{x_1 \cdots x_n}\]\[H(x_1, \ldots, x_n) = \frac{n}{\frac{1}{x_1} + \cdots + \frac{1}{x_n}}\]Realizar una función que calcule la mediana de una lista de números (el argumento en este caso es del tipo
list). La mediana se define como el valor para el cual la mitad de los valores de la lista es menor que ella. Si el número de elementos es par, se toma el promedio entre los dos adyacentes.
Realizar los cálculos para las listas de números:
L1 = [6.41, 1.28, 11.54, 5.13, 8.97, 3.84, 10.26, 14.1, 12.82, 16.67, 2.56, 17.95, 7.69, 15.39] L2 = [4.79, 1.59, 2.13, 4.26, 3.72, 1.06, 6.92, 3.19, 5.32, 2.66, 5.85, 6.39, 0.53]
La moda se define como el valor que ocurre más frecuentemente en una colección. Note que la moda puede no ser única. En ese caso debe obtener todos los valores. Escriba una función que retorne la moda de una lista de números. Utilícela para calcular la moda de la siguiente lista de números enteros:
L = [8, 9, 10, 11, 10, 6, 10, 17, 8, 8, 5, 10, 14, 7, 9, 12, 8, 17, 10, 12, 9, 11, 9, 12, 11, 11, 6, 9, 12, 5, 12, 9, 10, 16, 8, 4, 5, 8, 11, 12]
.
Funciones y decoradores
Hemos visto que en Python todo es un objeto, con lo cual, incluso las funciones, son objetos. Como tales tienen métodos y atributos:
lio_messi = "Lio Messi"
print(type(lio_messi))
<class 'str'>
La variable lio_messi es un string, y como tal, pertenece a la clase
str, que tiene sus propios atributos y métodos:
Veamos qué pasa con las funciones:
def saluda_a(alguien):
saludo = f"Hola {alguien}!"
return saludo
print(saluda_a(lio_messi))
Hola Lio Messi!
print(type(saluda_a))
<class 'function'>
Un atributo interesante de las funciones es __name__ por razones
que veremos en breve:
print(saluda_a.__name__)
saluda_a
Es decir, __name__ es el nombre de la función, que está guardado
dentro del objeto que representa dicha función. > La capacidad del
lenguaje de responderse preguntas sobre las propias entidades que
componen el lenguaje se llama introspección.
En la clase anterior vimos dos características importantes de las funciones en Python. La primera de ellas es que las funciones pueden retornar (esto es, crear) otras funciones:
def genera_recta(a,b):
"Genera la función recta y = a x + b"
def recta(x):
"Evalúa la función recta en x"
y = a * x + b
return y
return recta
f = genera_recta(2,3) # f(x) = 2 * x + 3
x = 2
print(f"f({x}) = {f(x)}") # f(2) = 2 * 2 + 3
x = 0
print(f"f({x}) = {f(x)}") # f(0) = 2 * 0 + 3
f(2) = 7
f(0) = 3
print(type(f))
<class 'function'>
La segunda de ellas es que es posible pasar como argumento una función a otra:
g = genera_recta(1,-1) # g(x) = x - 1
x = 3
y = f(g(x))
print(f"y = {y}")
y = 7
print(type(g))
<class 'function'>
Funciones que aceptan y devuelven funciones (Decoradores)
Vamos a trabajar ahora con los decoradores. Los decoradores no son otra cosa que funciones, pero que, por sus características, adquieren ese nombre y una forma particular de llamarlos que reduce convenientemente la sintaxis al programar. Empecemos por definir una función que devuelve otra función, como vimos arriba, de la siguiente forma:
def mi_decorador(func):
def wrapper():
print(f"Por llamar a la función {func.__name__}")
func()
print(f"Listo, ya llamé a la función {func.__name__}")
return wrapper
Definamos ahora un saludo genérico:
def saluda():
print("Holaa!!")
saluda()
Holaa!!
Nada nuevo hasta ahora, pero empecemos a combinar las funciones:
saluda_w = mi_decorador(saluda)
saluda_w()
Por llamar a la función saluda
Holaa!!
Listo, ya llamé a la función saluda
print(type(saluda_w))
<class 'function'>
Tenemos ahora una función saluda y su versión decorada
saluda_w, que simplemente llama a la función saluda, pero además
imprime mensajes antes y después del llamado a la función. Esto es algo
que uno va a querer hacer, por ejemplo para calcular el tiempo de
ejecución de una función, o para imprimir mensajes de registro
(logging) o debug, u otras tantas cosas más. Por eso Python introduce
una notación especial para este tipo de funciones mi_decorador:
saluda = mi_decorador(saluda)
@mi_decorador
def saluda_en_ingles():
print("Hello!!")
Notar que el decorador siempre empieza con el símbolo ``@`` y se
encuentra en la línea inmediatamente anterior a la definición de la
función.
saluda_en_ingles()
Por llamar a la función saluda_en_ingles
Hello!!
Listo, ya llamé a la función saluda_en_ingles
Qué pasa si queremos aplicar el decorador a una función que recibe
argumentos como saluda_a?
@mi_decorador
def saluda_a(alguien):
print(f"Hola {alguien}!")
saluda_a("Lio Messi")
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[21], line 1
----> 1 saluda_a("Lio Messi")
TypeError: mi_decorador.<locals>.wrapper() takes 0 positional arguments but 1 was given
Notemos que como está definido el decorador, recibe una función sin argumentos:
def mi_decorador(func):
def wrapper():
print(f"Por llamar a la función {func.__name__}")
func()
print(f"Listo, ya llamé a la función {func.__name__}")
return wrapper
En este último caso, al aplicar @mi_decorador a
saluda_a(alguien), estamos pasando a la función mi_decorador una
función func que dentro de mi_decorador se llama como
func(), es decir, no tiene argumentos. Para resolver este problema,
tenemos que indicar explícitamente que la función que vamos a llamar
dentro del decorador puede tener argumentos:
def mi_nuevo_decorador(func):
def wrapper(*args, **kwargs):
print(f"Por llamar a la función {func.__name__}")
func(*args, **kwargs)
print(f"Listo, ya llamé a la función {func.__name__}")
return wrapper
Hasta ahora la función func que envuelve el decorador no devuelve
ningún valor, sólo imprime un mensaje en pantalla. Cómo hacemos para
usar un decorador con una función que devuelve un valor?
def proto_debug_decorator(func):
def wrapper(*args, **kwargs):
print(f"Por llamar a la función {func.__name__}")
resultado = func(*args, **kwargs)
print(f"Listo, ya llamé a la función {func.__name__}")
return resultado
return wrapper
@proto_debug_decorator
def mi_calculo_complicado(x,y,z=0):
return x**2 + y**2 + z**2
v = mi_calculo_complicado(1,2,3)
print(v)
Por llamar a la función mi_calculo_complicado
Listo, ya llamé a la función mi_calculo_complicado
14
Decoradores, un ejemplo más útil
Recordemos que al llamar una función, *args representa a la tupla de
argumentos mientras que **kwargs es el diccionario de argumentos
opcionales. Escribamos un par de funciones útiles para transformar estos
tipos en string, de modo que se puedan imprimir, por ejemplo:
def args_as_str(*args, **kwargs):
args_str = ", ".join([str(a) for a in args])
kwargs_str = ", ".join([f"{k}={v}" for k,v in kwargs.items()])
return f"{args_str}, {kwargs_str}"
args_as_str(1,3,hola="Hello", a = 5 )
'1, 3, hola=Hello, a=5'
def debug_me(func):
def wrapper(*args, **kwargs):
print(f"{func.__name__} ({args_as_str(*args, **kwargs)})")
resultado = func(*args, **kwargs)
print(f"Listo, ya llamé a la función {func.__name__}")
return resultado
return wrapper
@debug_me
def mi_calculo_recontracomplicado(x,y,z=0):
return x**2 + y**2 + z**2
v = mi_calculo_recontracomplicado(1,2,z=3)
mi_calculo_recontracomplicado (1, 2, z=3)
Listo, ya llamé a la función mi_calculo_recontracomplicado
print(v)
14
Ejercicios 05 (c)
El módulo time calcula el tiempo en segundos desde el comienzo de la era de la computación (?), que para los fines prácticos, da inicio el 1 de enero de 1970 ;-D. Veamos unos ejemplos de su uso:
import time
ahora = time.time()
print (ahora)
# duerme 5 segundos
time.sleep(5) # zzzz.....
ahora = time.time()
print (ahora)
1740427615.6264267
1740427620.6271527
Utilizando las funciones anteriores, escriba el decorador @time_me
que calcula e imprime el tiempo que tarda en ejecutarse una función.
No empiece desde cero!! Use como plantilla para empezar el decorador
@debug_me y modifíquelo adecuadamente.
# descomente el decorador una vez que lo tenga programado
# @time_me
def mi_calculo_recontralargo(n):
l= [x for x in range(n)]
return sum(l)
mi_calculo_recontralargo(20000000)
199999990000000
Programación funcional con Python
La programación funcional es un paradigma de programación, de la misma manera que otros paradigmas, como la programación orientada a objetos, o la programación estructurada.
Existen lenguajes de programación que son directamente funcionales, esto es, implementan las reglas de la programación funcional directamente (por ejemplo, Lisp, Haskell, F#, etc.). Desde un punto de vista histórico, la programación funcional tiene su origen en la visión de Alonzo Church del problema de la decisión (Entscheidungsproblem), y es complementaria a la más conocida, propuesta por Alan Turing.
Python es un lenguaje orientado a objetos (todo elemento del lenguaje es un objeto), de modo tal que no es posible hablar de un paradigma funcional en Python, sino mas bien de un estilo de programación funcional.
Un trabajo interesante es el siguiente: ’Why Functional Programming Matters: http://www.cse.chalmers.se/~rjmh/Papers/whyfp.pdf”.
Los errores al programar
En el continuo devenir de la programación, uno se encuentra, principalmente, resolviendo errores. Un resumen de los errores posibles en un código se pueden encontrar en la expresión
i = i+1
En esta expresión podemos encontrar tres tipos de errores:
Error de lectura : el valor de
ien el lado derecho no es el que efectivamente uno desearía, es decir, el código está leyendo un valor incorrecto.Error de escritura : el valor de
ien el lado izquierdo no es el que efectivamente uno desearía, es decir, estamos guardando la expresión en una variable incorrecta.Error de cómputo : que se produce, por ejemplo, porque no queremos sumar 1 sino 2, o queremos restar el valor de i.
Existe un cuarto tipo de error que aparece y tiene que ver con un error de flujo, en el cual el código se ejecuta en una rama que no es la deseada, debido a que una condición lógica no se cumple tal como se esperaba. O por ejemplo, el orden en que se ejecutan las sentencias no es el adecuado:
# Función que calcula (x+1)(x+2)
def f(x):
x = x+1
y = x+1
return x*y
# Función que calcula (x+1)(x+2) ?? Mmmm.....
def g(x):
y = x+1
x = x+1
return x*y
print(f(3))
print(g(3))
20
16
Los errores en notebooks
Además de las complejidades propias de la programación, que están asociadas al dominio donde se encuentra el problema que uno quiere resolver, y a las dificultades que eso implica; los notebooks introducen también una dificultad adicional: uno puede redefinir los datos en celdas posteriores, pero puede volver ‘atrás’ en el código y recalcular otra celda. Veamos un ejemplo:
data = [1,2,3,4]
def prom(a):
s = sum(a)
n = len(a)
return s/n
prom(data)
2.5

Más código
data = "Some data"
print(len(data))
9
Mutabilidad
Los problemas que vemos arriba se deben a la mutabilidad: las variables pueden cambiar (esto es, ser reescritas) a lo largo del código. Ahora bien, pareciera que la mutabilidad es intrínseca a la computación, al fin y al cabo, en el hardware hay una cantidad limitada de memoria y de registros que son continuamente reescritos para que nuestro código corra. Sin embargo, los lenguajes de programación de alto nivel que usamos nos alejan (afortunadamente) del requerimiento de mantener el estado de la memoria y los registros explícitamente en el código (y en el algoritmo en nuestra cabeza).
La pregunta que cabe entonces es ¿cómo hacer un código que prevenga la mutabilidad, pero que a la vez me permita transformar los datos para resolver mi problema? La respuesta viene de la mano de un ente muy conocido en mátemáticas: las funciones
Funciones
Una función desde el punto de vista matemático es una relación que a cada elemento de un conjunto le asocia exactamente un elemento de otro conjunto. Estos conjuntos pueden ser números, vectores, matrices en el mundo matemático,
y = f(x)
y = f(x)
o, en un mundo más físico, peras, manzanas, nombres, apellidos, objetos varios:
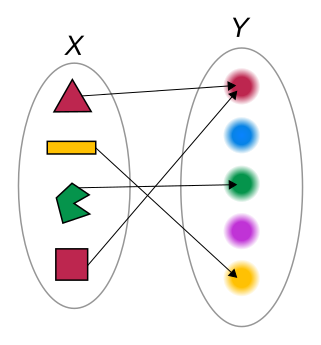
una funcion
Estas funciones tienen dos características fundamentales para usar en programación: - Permiten “transformar” un valor en otro - El valor original no se modifica
Es decir que el uso de funciones, al estilo matemático, en un código resuelven el problema de la mutabilidad, pero a la vez me permiten “transformar”, es decir, crear nuevos valores a partir del valor original.
Funciones puras
El análogo computacional de las funciones matemáticas se llaman funciones puras. Una función se dice pura cuando: - Siempre retorna el mismo valor de salida para el mismo valor de entrada - No tiene efectos colaterales (side effects)
una funcion
Funciones de primer orden o primera clase
Un lenguaje se dice que tiene funciones de primera clase cuando son tratadas exactamente igual que otros valores o variables.
Funciones de orden superior
Un lenguaje que permite pasar funciones como argumentos se dice que acepta funciones de orden superior.
def square(x):
return x*x
def next(x):
return x+1
a = 4
b = next(a)
c = next(next(a))
print(a)
print(b)
print(c)
4
5
6
def h(x):
return (next(x))*(next(next(x)))
print(h(3))
20
Si se tiene funciones puras, es posible componerlas
def compose(f, g):
return lambda x: f(g(x))
next2 = compose(next,next)
print(next2(a))
6
Inmutabilidad
Usando funciones puras se garantiza la inmutabilidad de los valores hacia adentro de la función. Pero, ¿qué sucede afuera? Python, al no ser un lenguaje funcional per se, no tiene la capacidad de establecer la inmutabilidad de cualquier valor, excepto para los casos de strings y tuplas, además, obviamente, de las expresiones literales.
Queda entonces en el programador la responsabilidad de no mutar los datos…
… o usar anotaciones de tipos
def cube(x: int) -> int:
return x*x*x
print(cube(2))
8
Nótese que Python NO chequea los tipos de datos, no tiene manera en
forma nativa de hacerlo. Por eso puedo ejecutar la función cube con
floats, por ejemplo:
print(cube(3.0))
27.0
No más loops
Si las funciones deben ser puras, y las ‘variables’ dejan de ser
variables y pasan a ser valores, entonces no puede haber loops en mi
código. Un loop necesita invariablemente un contador (i = i+1) que
necesariamente es una variable mutable. Así que así nomás, de un plumazo
no existen más loops.
¿Entonces? Entonces, todos los loops se reemplazan por llamados a funciones recursivas, o se utilizan funciones de orden superior:
# Filter
l = [1,2,3,4,5,6]
def es_par(x):
return (x%2 == 0)
pares = list(filter(es_par,l))
print(pares)
[2, 4, 6]
# Filter usando list comprehension
list(x for x in l if es_par(x))
[2, 4, 6]
# Map
siguientes = list(map(next,l))
print(siguientes)
[2, 3, 4, 5, 6, 7]
El módulo functools provee la función reduce, que complementa a
map y filter.
# Reduce
from functools import *
import operator
# Suma usando el predicado desde el módulo `operator`
suma = reduce(operator.add,l,0)
print(suma)
21
help(reduce)
Help on built-in function reduce in module _functools:
reduce(...)
reduce(function, iterable[, initial], /) -> value
Apply a function of two arguments cumulatively to the items of an iterable, from left to right.
This effectively reduces the iterable to a single value. If initial is present,
it is placed before the items of the iterable in the calculation, and serves as
a default when the iterable is empty.
For example, reduce(lambda x, y: x+y, [1, 2, 3, 4, 5])
calculates ((((1 + 2) + 3) + 4) + 5).
# Suma usando el predicado como lambda
otra_suma = reduce(lambda x,y: x+y, l)
print(otra_suma)
21
# Suma definiendo la propia función suma
def add(x,y):
return x+y
y_otra_suma = reduce(add,l)
print(y_otra_suma)
21
La suma de los cuadrados de una lista:
suma_cuadrados = reduce(lambda x,y: x+y, map(square,l))
print(suma_cuadrados)
91
Ejercicios 05 (d)
Construya una función
partition(lst,predicate)que dada una listalsty una funciónpredicate, separe la listalsten dos: una lista que contiene los valores para los cuales la funciónpredicatedevuelveTrue, y otra lista que contiene los valores para los quepredicatedevuelveFalse:def is_even(x): return x % 2 == 0 numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] evens, odds = divide_list(numbers, is_even) print(evens) # Output: [2, 4, 6, 8, 10] print(odds) # Output: [1, 3, 5, 7, 9]
Dado la cadena de caracteres
s1='En un lugar de la Mancha de cuyo nombre no quiero acordarme'
Utilice
reduce,mapy/ofilter(y las funciones auxiliares necesarias) para:Obtener la cantidad de caracteres.
Imprimir la frase anterior pero con cada palabra empezando en mayúsculas.
Contar cuantas letras ‘a’ tiene la frase.
Contar cuántas vocales tiene.