Implementation of time-of-flight calculations

Diagrama de Tiempo de vuelo

Equations of motion

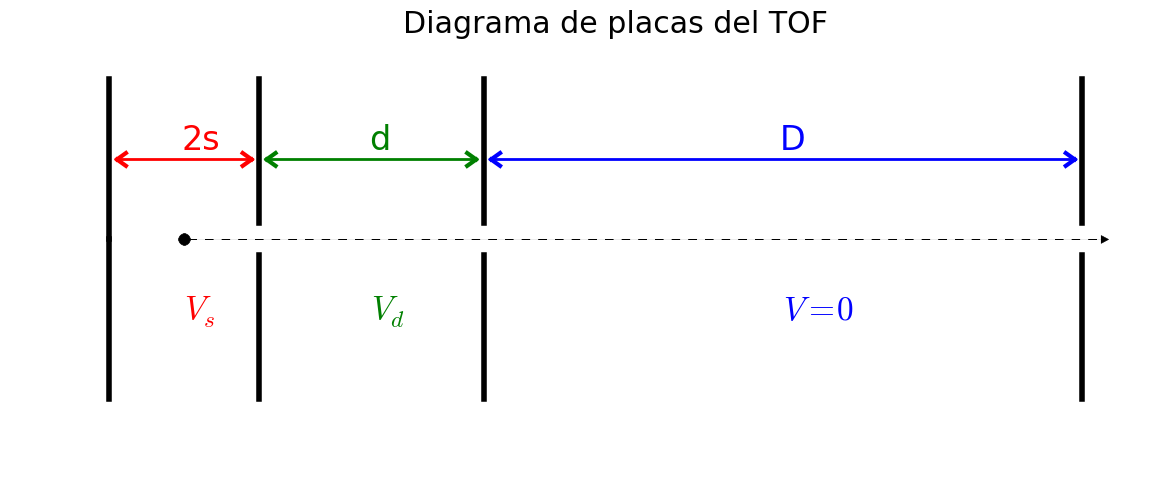
The equations of motion for each stage of the spectrometer are:

\[\begin{split}v &= v_{0} + a t \\ \Delta s &= v_{0} t + a t^{2}/2 \qquad (a = q E /m )\end{split}\]

By defining the dimensionless magnitudes

\[\begin{split}u &\equiv \sqrt{m} v \\ f &\equiv a/m = qE \,, \\ T &\equiv t/\sqrt{m}\end{split}\]

and solving for time, we get

\[T = \left[\sqrt{u_{0}^{2} + 2 \Delta s\, f} - u_{0}\right]/f\]

Time of flight for each stage is given by (\(t_{j} = \sqrt{m}\,T_{j}\)):

\begin{align*} T_{s} &= \left[\sqrt{u_{0}^{2} + 2 (s_{0} - x_{0})\, q E_{s}} - u_{0}\right]/(q E_{s}) & u_{s} &= u_{0} + q \,E_{s} T_{s} \\ T_{d} &= \left[\sqrt{u_{s}^{2} + 2\, q\,d E_{d}} - u_{s}\right]/(q E_{d}) & u_{d} &= u_{s} + q\, E_{d} \,T_{d} \\ T_{D} &= D/u_{d} \end{align*}

Initial conditions

  • Initial velocities are given by the Maxwell-Boltzmann distribution in the direction of the TOF

    \[P(u_{0}) = \frac{1}{\mathcal{Z}}\, e^{-u_{0}^{2}/2k_{B}T}\]

    with width \(\sigma = \sqrt{k_{B} T}\)

  • The spatial distribution may be chosen either uniform with width \(\delta s\), or normal with \(\sigma= \delta s/2\).

  • The time distribution also may be chosen either uniform of width \(\delta t\), or normal with \(\sigma= \delta t/2\). The default value is \(\delta t= 8~\mathrm{ns}\).