Decaímiento espontáneo de estados metaestables
Decaímiento espontáneo de estados metaestables
Definición del problema
Cuando una partícula (núcleo, átomo, o molécula) se encuentra en un estado que no es estable, puede decaer espontánemente. Por ejemplo, algunos núcleos decaen a otros emitiendo radiación \(\alpha\), \(\beta\) o \(\gamma\). Otro ejemplo es el de átomos, que pueden decaer a un estado más estable emitiendo luz o electrones.
La probabilidad de decaímiento de cada partícula en un intervalo de tiempo \(\Delta t\) es constante. Además, cada partícula actúa independientemente, o sea que el decaímiento de una dada partícula no influye en las otras partículas. Por lo tanto, el número de partículas que decaen en un instante dado es proporcional al número total de partículas. O sea que si la probabilidad por unidad de tiempo de que una partícula decaiga tiene el valor constante \(P\), el número de partículas que decaen será
Si en un instante \(t_0\) dado tenemos \(N(t_{0})\) partículas y en el intervalo \(\Delta t\) decaen \(N_d\) partículas, claramente a tiempo \(t_0 + \Delta t\) tendremos \(N(t_0 + \Delta t) = N(t) - N_d\) partículas.
Utilizando que \(N_d\) es proporcional a \(N\) (ecuación (1)) obtenemos una ecuación para el número de partículas que quedan como función del tiempo:
o, equivalentemente para el el cambio en el número de partículas por unidad de tiempo \(\Delta N / \Delta t\)
Este ejercicio propone estudiar mediante simulaciones la evolución en el tiempo del número \(N(t)\) de partículas en una caja que decaen espontáneamente. Para ello se pide:
Enunciado
Etapa 1
Escribir un programa que simule el decaimiento espontáneo de \(N\) partículas en una caja y permita obtener el número de partículas como función del tiempo.
Graficar el número de partículas \(N(t)\) y de la diferencia \(\Delta N\) como función del tiempo \(t\) para distintos valores del número inicial de partículas \(N_0=10, 100, \dots, 100000\) (logarítmicamente espaciado).
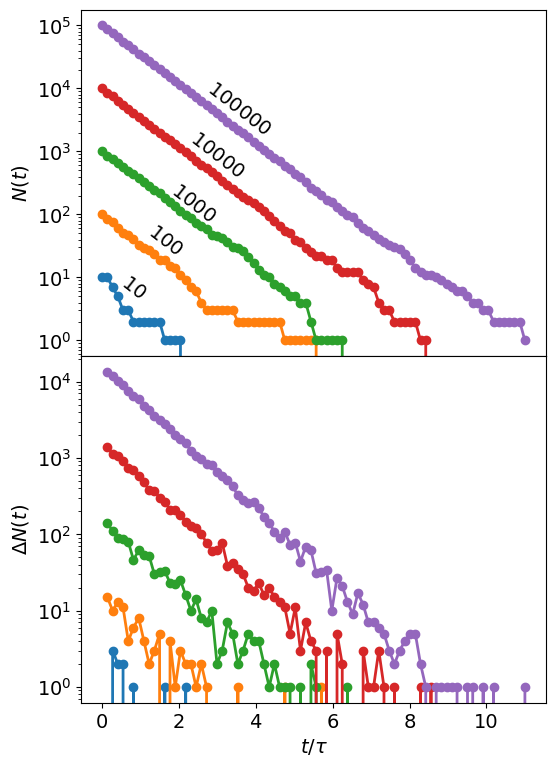
Ejemplo de gráfico
Ajuste los valores de \(N(t)\) suponiendo que tiene un comportamiento del tipo:
\(f(t) = A t^{\alpha}\)
\(f(t) = B e^{- \lambda t}\)
para cada valor de \(N\), encuentre cuál da un mejor ajuste y relacione los resultados obtenidos para las constantes con los parámetros del problema \(N_0\) y \(P\).
Nota
Considere valores de la probabilidad por unidad de tiempo adecuados. En la figura se usó un valor \(P \cdot \Delta t \approx 0.13\)
Etapa 2
Ahora modificamos levemente la física del problema. Considere que cuando cada partícula decae emite un electrón con una energía media igual a 10 eV. que se mide con un detector que se encuentra a una distancia de 1 m. La energía del electrón emitido tiene una distribución Gaussiana con ancho \(\sigma\) igual al 10% de su energía media. Considere sólo un valor de \(N_0\) (tome \(N_0 = 10^5\) o \(10^6\)).
Consejo
Recuerde que el paquete Scipy tiene un módulo con definiciones de unidades y constantes matemáticas y físicas
El detector tiene un área dada y es del tipo centellador. Cada vez que detecta un electrón se ilumina la posición a la que el electrón llega. Simule cómo se vería el detector en estas condiciones, donde en función del tiempo se van detectando nuevas partículas.
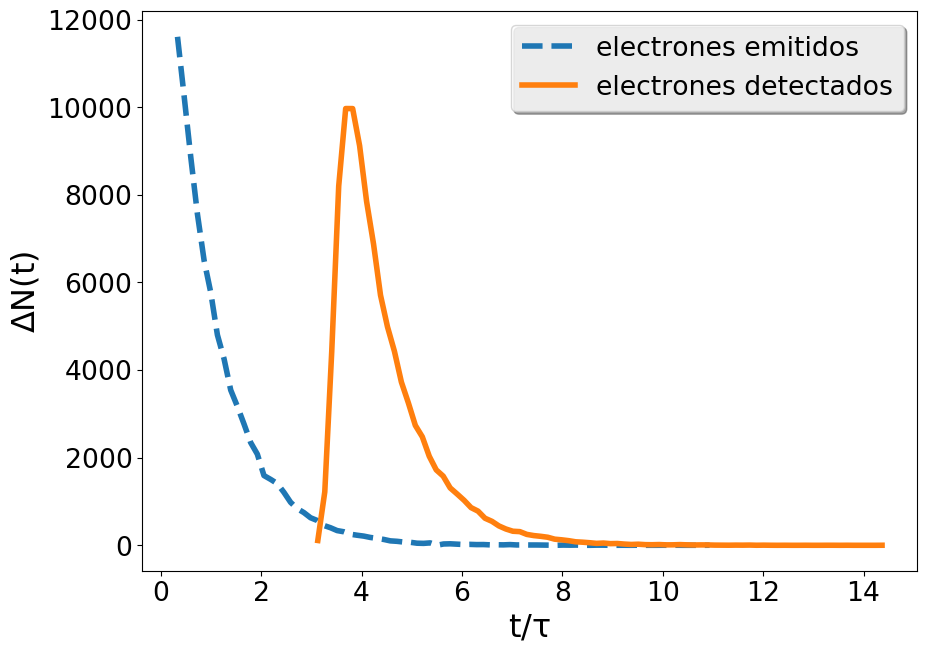
Simular el número de electrones detectados por unidad de tiempo en estas condiciones. La probabilidad por unidad de tiempo es \(P=3.2 \times 10^{6}\). Grafique el número de electrones detectados y emitidos como función del tiempo, como se muestra en la figura:
Etapa 3
Calcule el punto anterior cuando, en lugar de tener un detector pequeño a la distancia de 1 m, se quiere saber el contaje por unidad de tiempo en una pared infinita localizada en esa posición (el problema ya no tiene simetría esférica).